Pisałam już o wprowadzaniu ułamków i ich porównywaniu. Są to niesamowicie ważne doświadczenia, stanowiące fundament do dalszej pracy z ułamkami dziesiętnymi. To właśnie na samym początku poznawania ułamków dziesiętnych dziecko musi doświadczyć, że te ułamki dziesiętne stanowią naturalne uzupełnienie systemu dziesiętnego, pozwalające nie tylko na zliczanie całości, ale również jej części. Jeśli wie, że z częściami dziesiątymi, setnymi czy tysięcznymi jest “tak samo” jak z tysiącami, setkami, dziesiątkami i jednościami, to nie powinno mieć wielkich problemów w poszerzeniu działań na liczbach naturalnych również na ułamki dziesiętne. Pojawią się oczywiście wyzwania. Na przykład, by uświadomić sobie, że “wyrównywanie liczb do prawej”, które było pierwszym elementem dodawania i odejmowania pisemnego, musimy zastąpić “wyrównywaniem przecinka”. Albo żeby pamiętać, że w ułamkach dziesiętnych brak jakiejś cyfry możemy “zapełnić” zerem. Ale po kolei… 🙂
Jeśli chcesz zobaczyć (a nie tylko przeczytać opis) pracę na materiale, to zachęcam do zakupienia nagrania video, zawierającego prezentację krok po kroku wszystkich czterech podstawowych działań na ułamkach dziesiętnych. To ponad 3 godziny nagrania, wypełnionego konkretami.
Nie dodawać kaczek do litrów wody
Kluczową trudnością w dodawaniu i odejmowaniu ułamków dziesiętnych jest zrozumienie znaczenia każdej z cyfr i dodawanie tylko odpowiednich pozycji w systemie dziesiętnym (całości do całości, części dziesiąte do dziesiątych, setne do setnych itd.). Doskonale pomaga w tym montessoriański materiał – jeśli operujemy na nim, odejmowanie czy dodawanie w odpowiedni sposób będzie naturalne.
Jeśli umiemy ułożyć ze znaczków składniki sumy, którą chcemy policzyć, to dodawanie staje się proste – wystarczy zliczyć łączną liczbę znaczków każdego rodzaju. Nie dodamy przecież niebieskich znaczków do zielonych – nie dość, że mają inny kolor, to jeszcze leżą na innych polach planszy. Materiał prowadzi nas za rękę przez proces dodawania czy odejmowania 🙂 Czasem tylko potrzebne będzie dokonanie zamian (wymiana 10 znaczków na 1 o większej wartości przy dodawaniu lub “rozmienianie-pożyczanie” w przypadku odejmowania). Warto jednak zostawić te bardziej złożone przykłady na później i stopniować trudność 🙂
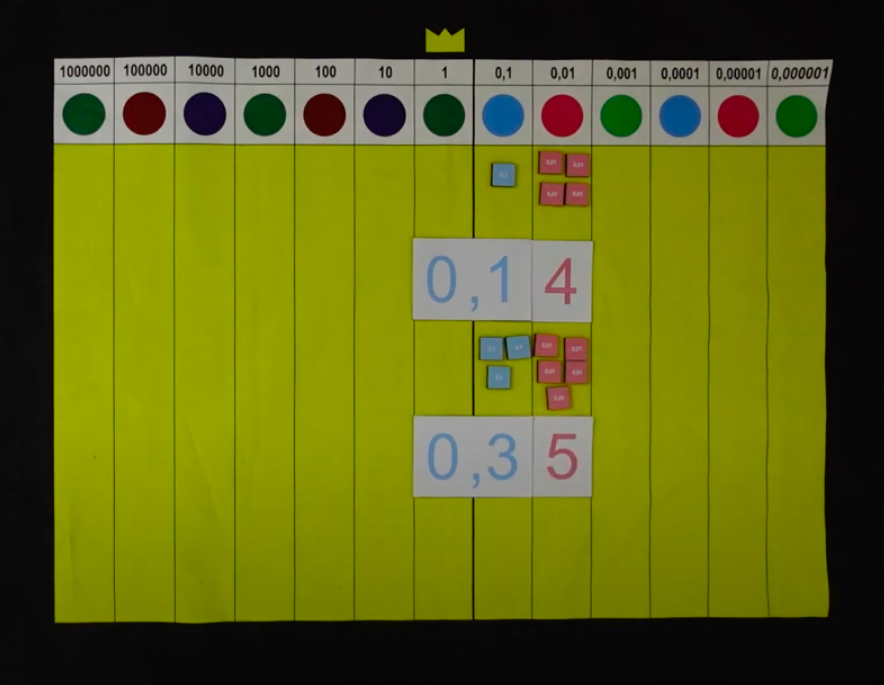
Jeśli zbierzemy doświadczenia z materiałem, łatwo się potem do nich odwołać, gdy przejdziemy do abstrakcyjnej pracy.
Gdy jedna z liczb jest “dłuższa”…
Przy abstrakcyjnych obliczeniach dzieci łatwo mylą się, wyrównując przy pisemnym odejmowaniu lub dodawaniu liczby do prawej strony – tego przecież przyzwyczaiły się przy liczbach naturalnych. Na materiale takie pomyłki zdarzają się zdecydowanie rzadziej – tabliczki do podpisów i same znaczki niejako wymuszają zastanowienie się nad znaczeniem poszczególnych cyfr. A kiedy już je mamy w rękach, oczywiste jest, że brak cyfry niczym nie różni się od cyfry zero – po prostu na danej pozycji nie ma znaczków!
I choć czasem nadal stanowi to wyzwanie, to odwołanie się do konkretu rozwiewa wiele wątpliwości i pozwala samodzielnie odkryć metodę postępowania.
A przekraczanie progu…? Jak sobie poradzić?
Początkowo wyzwanie może stanowić również przekraczanie progu dziesiątkowego. To dlatego warto rozpocząć od przykładów, które go nie wymagają. Mimo to przekraczanie progu dziesiątkowego nie stanowi poważnego kłopotu – przecież dziecko umie już sobie z nim poradzić przy liczbach naturalnych, a z ułamkami dziesiętnymi jest… tak samo!

Dlatego właśnie tak dużą wagę przywiązuję do etapu wprowadzania ułamków dziesiętnych – jeśli dziecko wie, jakie zasady rządzą poszczególnymi pozycjami w systemie dziesiętnym, bez trudu rozszerzy umiejętności dotyczące liczb naturalnych również na ułamki dziesiętne. A jeśli masz poczucie, że warto pogłębić ten wczesny etap i ze spokojem wejść w działania na ułamkach, zapraszam do filmu o wprowadzeniu w świat ułamków dziesiętnych:
Przejście do abstrakcji
Przejście od pracy na materiale do abstrakcyjnego rozwiązywania zadań na kartce jest stopniowe. Bardzo wspierają je odpowiednio dobrane zadania. Ja zebrałam takie z bazach, które można pobrać tutaj:
Pierwsze dwie bazy zawierają dodawanie i odejmowanie z przygotowanym już zapisem pisemnym, w kolejnych dwóch – wymagających zapisania działania pisemnie przez dziecko. W kolejnych częściach każdej z tych baz znajdziemy przykłady stopniujące trudność:
- z liczbami zawierającymi tyle samo cyfr po przecinku, bez przekraczania progu dziesiątkowego (tu możemy skupić się z dzieckiem na odkryciu, że dodawanie ułamków dziesiętnych “działa tak samo” jak w przypadku liczb naturalnych)
- z liczbami zawierającymi różną liczbę cyfr po przecinku, bez przekraczania progu dziesiątkowego (tutaj skupiamy się na trudności, jaką jest odpowiednie wyrównywanie liczb i dodawanie odpowiednich części)
- z liczbami zawierającymi tyle samo cyfr po przecinku, z przekraczaniem progu dziesiątkowego (tu skupiamy się na przekraczaniu progu, zapominając na chwilę o poprzedniej trudności)
- z liczbami zawierającymi różną liczbę cyfr po przecinku, z przekraczaniem progu dziesiątkowego (to moment, gdy pokonujemy obie trudności naraz i… wiemy już wszystko!).
Jeśli chcesz zobaczyć i usłyszeć więcej, możesz wykupić dostęp do nagrania, na którym opowiadam o wszystkich działaniach na ułamkach dziesiętnych. A może zdecydujesz się na pakiet, w którym zawarłam również wiedzę o wprowadzeniu ułamków dziesiętnych? Zapraszam! 🙂




