Świat liczb “po drugiej stronie jedności”, czyli wprowadzamy ułamki dziesiętne

Pisałam już kiedyś o wprowadzaniu ułamków dziesiętnych. Skupiłam się w nim na wprowadzeniu nazewnictwa i odczytywaniu ułamków. Dziś kolejny wpis wokół wprowadzania ułamków dziesiętnych, bo jest to temat dużo obszerniejszy, niż nam się często wydaje. Tym razem skupiam się na tym, by “poczuć” jaką wartość kryją w sobie części dziesiąte, setne, tysięczne, dziesięciotysięczne… Zapraszam!

A jeśli wolisz posłuchać i popatrzeć, to możesz skorzystać z nagranego przeze mnie filmu. Zawarłam na nim wszystko, co dotyczy wprowadzania ułamków dziesiętnych, ich “wyczucia” i nazywania.

Świat po drugiej stronie jedności

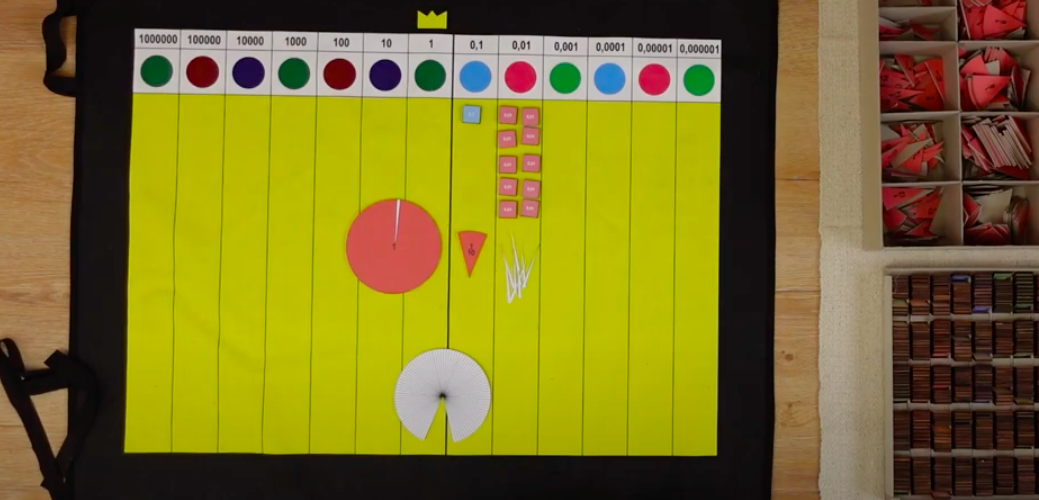
Podstawową kwestią w odkrywaniu ułamków dziesiętnych jest zobaczenie, że stanowią one naturalne uzupełnienie systemu dziesiętnego. Warto od tego zacząć! Weźmy tysiąc (może być znaczek, może być tysiąc ze złotego materiału) – jeśli mamy taką możliwość umieśćmy go na macie. Zapytajmy dziecko, na co możemy go rozmienić, lub sami zaprezentujmy zamianę na dziesięć setek, umieszczając je na macie w miejscu do tego przeznaczonym. Weźmy teraz jedną z setek i znów rozmieńmy, tym razem na dziesięć dziesiątek. Dziesiątkę rozmieńmy na dziesięć jedności.

Teraz kluczowy moment – czy możemy rozmienić jedność, znów na dziesięć mniejszych elementów? Tu dziecko znające ułamki zwykłe może zaproponować części dziesiąte – jeśli tak, to “podłapmy” ten pomysł i to wykorzystajmy! Nawet jeśli używamy znaczków do ułamków dziesiętnych, możemy od początku podkreślać, że to “te same” części dziesiąte. A jeśli dziecko uważa, że nie można rozmienić jedności? Opowiedzmy mu o tym, że moglibyśmy podzielić jedność tak jak dzielimy tort czy jabłko. Ponieważ działamy w systemie dziesiętnym, rozmienimy właśnie na dziesięć części. Wtedy rozmieńmy jedność na dziesięć części dziesiątych (warto wykorzystać do tego znaczki). Podkreślmy, że są to części dziesiąte.

Kolejnym krokiem jest opowieść o tym, że możemy tak rozmieniać dalej i dalej – jedną z części dziesiątych możemy rozmienić na dziesięć mniejszych. Nazywamy je częściami setnymi (dlaczego akurat setne? to temat na jeszcze jedną opowieść… ;)). Część setną możemy rozmienić na kolejne – części tysięczne. Tak samo część tysięczną możemy rozmienić na dziesięć części dziesięciotysięcznych. I tak dalej… części stutysięczne i milionowe (i kolejne też, tyle że zwykle nie mamy już dla nich znaczków ani miejsca na macie – ale przecież moglibyśmy mieć!).

Rozmieniać możemy też na jeszcze mniejsze części. Ważnym doświadczeniem jest zobaczenie, że każdy znaczek możemy rozmienić na sto znaczków z pozycji dziesiętnej “o dwa w prawo” – wystarczy że rozmienimy je na dziesięć znaczków z kolejnej pozycji, a każdy z nich rozmienimy na dziesięć jeszcze kolejnej. A więc nie tylko setka to sto jedności. Wiemy też, że dokładnie na tej samej zasadzie dziesiątka to sto części dziesiątych, jedność na sto części setnych (“a więc to dlatego to są części setne!”), część dziesiątą na sto części tysięcznych, część setną na sto części dziesięciotysięcznych i tak dalej. Kolejnym krokiem będzie dostrzeżenie, że każdy znaczek możemy rozmienić na tysiąc znaczków z pozycji dziesiętnej “o trzy w prawo”. Te zamiany będą nam potrzebne bardzo szybko, choćby przy odczytywaniu ułamków dziesiętnych.

Tak powstaje nam świat “po drugiej stronie jedności”. Nie służy on do opisywania, ile mamy jedności (tak jak jedności, dziesiątki, setki, tysiące), ale do opisywania kawałków jedności. Jakimi prawami rządzi się ten świat? W wielu kwestiach – dokładnie takimi samymi jak ten “zwykły” świat liczb. Dziesięć elementów tego samego rodzaju można wymienić na jeden wyższego rzędu. I odwrotnie – każdy element można zamienić na dziesięć elementów niższego rzędu. Są jednak rzeczy, które mogą zaskakiwać “po drugiej stronie jedności”. Jest to na przykład układ kolorów i nazw – części dziesiąte są “w lewo” od części setnych, choć dziesiątki są “w prawo” od setek. Wszystkie nazwy “idą w drugą stronę”. I to jest bardzo, bardzo ważne! Wraz z nazwami kolejność zmieniają kolory. To dlatego, że kolory w montessoriańskim materiale powiązane są właśnie z nazwą: części dziesiąte i dziesięciotysięczne są błękitne (dziesiątki i dziesiątki tysięcy są granatowe), części setne i stutysięczne są różowe (setki i setki tysięcy są czerwone), a części tysięczne i milionowe są jasnozielone (jedności, tysiące i miliony są ciemnozielone).

Przepięknie można to pokazać, łącząc odpowiadające pola na macie. Jedność jest bez pary, możemy więc umieścić przy niej pionową linię – kolor zielony będzie nawiązywać do koloru jedności. Teraz dziesiątki i części dziesiąte łączymy niebieskim półokręgiem. Setki i części setne łączymy czerwonym półokręgiem (musi on być odpowiednio większy od poprzedniego). Tysiące i części tysięczne – zielonym półokręgiem. I tak dalej… Co powstało? Wielu osobom kojarzy się to ze świecznikiem przypominającym żydowską menorę (tylko ramion może mieć więcej, zależnie od rozmiaru naszej maty). Jeśli chcecie – możecie taki świecznik ustawić naprawdę, dodatkowo zawiązując na ramionach kolorowe kokardki lub wykorzystując kolorowe świece. Na pewno stworzy wyjątkową atmosferę, która wiele dzieci wspiera i zachęca do poznawania danego tematu.

Części dziesiąte i setne – małe czy duże?

Na początku spróbujemy doświadczyć, jak duże (a może jak małe?) są części dziesiąte i setne – jest to ważne doświadczenie niezależnie od tego, czy dziecko zna już ułamki zwykłe, czy nie. Spróbujmy!

Jednym ze sposobów prezentacji tej wartości jest wykorzystanie części koła, jak przy ułamkach zwykłych (bo to są “te same” części dziesiąte i setne!).

Do niektórych dzieci mocno przemawia wartość pieniężna. Jeśli za jedności uznamy złotówki, to części setne odpowiadają groszom, a części dziesiąte – dziesięciogroszówkom. Trochę myląca może być zbieżność dziesiątki na monecie z nazwą części dziesiątych, polecam więc uniknąć tego porównania na wczesnym etapie wprowadzania ułamków dzieciom, dla których może to stanowić problem. Pomimo tego taka prezentacja ma swoje zalety – wartość pieniędzy jest dla wielu dzieci bardzo obrazowa i konkretna.

Ja lubię pokazać jeszcze, że części dziesiąte mogą być niepozorne i łatwe do przegapienia, a jednocześnie znaczące, za pomocą… magicznej sztuczki! Z trzech wydrukowanych elementów układamy obrazek z siedemnastoma kurczakami. Następnie zamieniamy górne części miejscami i… na obrazku jest już tylko szesnaście kurczaków! Zaintrygowani? Spróbujcie sami 🙂

Jak można wyjaśnić tę zagadkę i co ma wspólnego z ułamkami dziesiętnymi? Już zdradzam 🙂

Zacznijmy od ułożenia, w którym na obrazku jest 16 kurczaków. Kurczaki, które w całości znajdują się na którymś z kawałków (jest sześć takich), pozostaną niezmienione przy przekładaniu kartek, zmienią tylko swoje miejsca. Możemy więc nie zwracać na nich uwagi. Przyjrzyjmy się pozostałym dziesięciu. Jeden z nich (piąty od lewej strony) w ogromnej części znajduje się na dolnej części kartki – na górną część wystaje tylko “kawałeczek”. Po przełożeniu elementów zostanie już bez tego “kawałeczka”, ale nadal będzie pełnoprawnym kurczakiem 🙂 A co stanie się z “kawałeczkiem”? Powędruje do innej “dolnej” części kurczaka, który wcześniej miał trochę większą górną część. A ta “trochę większa górna część” zastąpi taką jeszcze większą… I tak dalej aż do dziesiątego kurczaka, którego górna część stanie się… całym, jedenastym, kurczakiem! W taki sposób dziesięć niewielkich ubytków w kurczakach złożyło się na całego nowego.

Co to ma wspólnego z ułamkami dziesiętnymi? Te zmiany w kurczakach to mniej więcej części dziesiąte. Są stosunkowo niewielkie – przecież ich zabranie/dodanie do kurczaków nie wzbudzało naszego niepokoju i nie sprawiało, że kurczaki były niekompletne 😉 Z drugiej strony to właśnie z tych kawałków “uzbierał” się dodatkowy kurczak, widać więc że nawet takie niewielkie części mają w sobie moc!

Ile kryją w sobie części setne, tysięczne, milionowe…?

Jeśli mamy wyczucie, czym są części dziesiętne i setne, warto pójść dalej! Spróbujemy przekonać się, jak małe są części tysięczne, dziesięciotysięczne, stutysięczne i milionowe. Warto zacząć od tego, by odwołać się do porównań, które już mamy, na przykład:

• jeśli obserwowaliśmy fragmenty koła, zastanówmy się z dzieckiem, czy jesteśmy w stanie przeciąć część setną na dziesięć równych części…? Może być trudno 😉
• jeśli odwoływaliśmy się do monet, warto pokazać, że części setnych złotówki (groszy) nie możemy już bardziej rozmienić.

Spróbujemy więc trochę powiększyć jedność 😉 Ja wybrałam kwadrat metr na metr. Najwygodniej skleić go z papieru milimetrowego – jeśli nie masz takiego, to możesz wydrukować przygotowany przeze mnie plik. Potrzebne będzie 20 kartek – wycinamy zadrukowaną część i sklejamy w kwadrat. Przy sklejaniu zwróćcie uwagę, by grubsze linie były rozłożone regularnie, co dziesięć cieńszych.

Kiedy mamy przygotowany nasz kwadrat – jedność, przyjrzyjmy mu się i spróbujmy zaznaczyć jedną dziesiątą. Wystarczy zaznaczyć jedną dziesiątą jednego boku (w tym pomogą nam pogrubione linie) i narysować prostokąt na całą długość. Potem możemy zaznaczać kolejne części (polecam robić to obok tych już zaznaczonych, by łatwiej było je oznaczać):

• aby uzyskać jedną setną, musimy podzielić jedną dziesiątą na dziesięć części, najwygodniej będzie podzielić na dziesięć długość prostokąta odpowiadającego jednej setnej (otrzymamy kwadrat o boku jednego decymetra),
• część tysięczną naszej jedności otrzymamy, dzieląc na dziesięć część setną. Otrzymamy na przykład prostokąt centymetr na decymetr,
• część dziesięciotysięczna będzie kwadratem o boku centymetra. Wydaje się bardzo mała w porównaniu z całością, prawda? A to jeszcze nie koniec…
• część stutysięczna będzie prostokątem milimetr na centymetr,
• część milionowa będzie kwadratem o boku jednego milimetra. Malutkim wycineczkiem naszej ogromnej całości!

Warto po zakończonej pracy przyjrzeć się zaznaczonym częściom. Jak szybko maleją! To powód dla którego zwykle używamy tylko kilku pierwszych

Lewo – dużo, prawo – mało. Czy zawsze?

Po wcześniejszych ćwiczeniach mamy już dość mocne przekonanie, że im dalej w prawo wędrujemy na macie, tym mniejszą wartość mają poszczególne znaczki.

Może jednak jest tak, że razem z tych malutkich części możemy uzbierać całkiem pokaźną liczbę? Przekonamy się o tym przy zmodyfikowanej “grze w dziewięć” zaproponowanej przez samą Marię Montessori. Najlepiej wykonywać ją, gdy dziecko umie już nazywać ułamki dziesiętne i ma świadomość, że na każdym miejscu może być najwyżej dziewięć znaczków.

Zachęćmy dziecko do ułożenia na macie jak największej liczby, która jest złożona tylko z części ułamkowych (dziesiątych, setnych, tysięcznych itd.). Możemy mieć najwyżej 9 znaczków w każdej pozycji dziesiętnej, więc będzie to liczba 0,999999. Zapowiedzmy dziecku, że dodamy do niej tę najmniejszą część, jedną milionową. Dołóżmy ją i zaprezentujmy, co się stanie (lub poprośmy dziecko, by spróbowało dokonać odpowiednich zamian, by odczytać wynik).

• by odczytać wynik, nie możemy mieć dziesięciu znaczków części milionowych, dlatego musimy je wymienić na jedną część stutysięczną,
• ale teraz mamy dziesięć części stutysięcznych! Wymieniamy je na jedną część dziesięciotysięczną.
• Teraz dziesięć części dziesięciotysięcznych – musimy je wymienić na jedną część tysięczną,
• a dziesięć części tysięcznych wymieniamy na jedną część setną.
• Dziesięć części setnych stanie się jedną częścią dziesiątą, a…
• dziesięć części dziesiątych wymienimy na jedność.

Co to oznacza? Liczba 0,999999 po dodaniu jednej milionowej dała nam jedność. W takim razie 0,999999 jest liczbą mniejszą od jedności (choć “tylko troszeczkę” ;)). Największa liczba złożona z części ułamkowych nie może przekroczyć jedności! Tym bardziej inne liczby, które się składają tylko z ułamkowych części.

To bardzo ważne doświadczenie, które możemy jeszcze rozszerzyć, powtarzając ćwiczenie (w rzeczywistości lub abstrakcyjnie, jako eksperyment myślowy) dla elementów kończących się z innym miejscu maty (na przykład liczba 0,009999 po dodaniu jednej tysięcznej da nam jedną setną). Bardzo przyda się przy porównywaniu liczb!

Wolisz popatrzeć?

Niestety nie mam możliwości wykonania prezentacji “na żywo”, ale możecie zobaczyć, jak robię to na filmie 🙂 Pełne prezentacje wraz z komentarzami, opowiadające o wprowadzeniu ułamków dziesiętnych, przedstawieniu ich wartości oraz nauce właściwego nazywania.