Dzielenie pisemne to spory kłopot dla wielu uczniów. Często umyka z głowy, a sytuacji “szczególnych” zdarza się naprawdę sporo, choć wielu nauczycieli zdaje się o tym nie pamiętać. Dziś chciałabym pokazać, jak można dzielić wielkie liczby na konkrecie. Maria Montessori zaproponowała do tego celu “Laboratorium” – przepiękną pomoc, która umożliwia dzielić duże liczby (maksymalnie siedmocyfrową dzielną przez co najwyżej czterocyfrowy dzielnik).

Jest również doskonałym wprowadzeniem do dzielenia pisemnego, wykonywanego już abstrakcyjnie, na kartce.
Kiedy dziecko może rozpocząć dzielenie pisemne? Gdy tylko opanuje dzielenie z resztą w zakresie tabliczki mnożenia. Na konkrecie może działać już wcześniej – wówczas możemy uczyć zapisu dzielenia pisemnego, ale nie będzie jeszcze możliwe przejście do abstrakcji.
Montessoriańska pomoc do dzielenia – z czego będziemy korzystać?
Laboratorium jest niestety bardzo drogą pomocą i wśród tradycyjnych pomocy Montessori nie ma zamienników. Jeśli nie macie możliwości pożyczenia czy zakupu tej pomocy, zachęcam do wykonania własnej, wykorzystującej znaczki. Nie może to być tradycyjna “gra w znaczki” z dwóch powodów. Po pierwsze, w czasie dzielenia potrzebne jest do 100 znaczków jednego rodzaju (znacznie więcej niż w tradycyjnej pomocy). Po drugie, przy dzieleniu bardzo często “rozmieniamy” znaczki na drobniejsze – na tyle często, że ich odliczanie jest nużące i zniechęca dziecko do pracy.
Dlatego w mojej pomocy zobaczycie:
- ZNACZKI (po 100 sztuk każdego rodzaju, przynajmniej mniejszych rzędów). Koniecznie muszą mieć konkretną, jednakową grubość. Ja wydrukowałam wzór na papierze i nakleiłam na tekturę introligatorską 2mm, a w kolejnym podejściu – na sklejkę.
- PUDEŁKO, nie mniej ważne od znaczków. W każdym rzędzie znajdują się znaczki jednego rodzaju, pogrupowane po 10. Przegródki są wykonane w taki sposób, by umożliwić szybkie wyjęcie całej dziesiątki znaczków.

Jej wykonanie nie jest tak trudne, jak może się wydawać. Zachęcam, żeby spróbować! Jeśli nie macie takiej możliwości, po prostu przed rozpoczęciem pracy rozkładajcie znaczki na kupkach po 10, by móc szybko po nie sięgnąć.
Bierzemy się za dzielenie – wstęp
Opiszę dzielenie w wersji ze znaczkami. Osoby posiadające laboratorium powinny bez problemu przełożyć sobie opis na swoje potrzeby. Można go też że szczegółami znaleźć w książce prof. Sabiny Guz.
Żeby rozpocząć dzielenie, musimy przygotować sobie liczbę, którą chcemy dzielić (układamy ją ze znaczków) oraz tyle pionków, ile wskazuje dzielnik.
Żeby zrozumieć podstawy procesu dzielenia, zachęcam do tego by rozpocząć od dzielnej, w której każda cyfra jest podzielna przez dzielnik, np. od działania 693:3. Tłumaczymy dziecku, że każdy pionek musi otrzymać tyle samo. Tutaj łatwo to zrobić: każdy pionek dostanie 2 setki, 3 dziesiątki i 1 jedność, czyli 231. Właśnie ta liczba – wartość, którą otrzymał każdy pionek – jest wynikiem dzielenia.
Jeśli dziecko lubi dopytywać o szczegóły (np. przy dodawaniu pisemnym chciało zrozumieć, dlaczego wykonujemy je od prawej strony – o tym pisałam w artykule o dodawaniu), to jako następny zróbmy prosty przykład, który pokaże dlaczego dzielenie najszybciej wykonuje się od lewej do prawej. Poprośmy dziecko, by spróbowało teraz podzielić 156:3. Część dzieci zacznie od podzielenia 6 jedności (to można zrobić bez problemu), ewentualnie rozdzieli też 3 z 5 dziesiątek. Potem zacznie zastanawiać się nad pozostałością. Jeśli nie ma pomysłu, możemy przypomnieć mu o rozmienianiu znaczków. Jeśli rozmieni 2 dziesiątki, to będzie mógł każdemu z pionków dać po 6 jedności (ale 2 jedności nadal zostaną). Teraz jeśli rozmieni setkę, to każdy z pionków otrzyma 3 dziesiątki i 1 dziesiątka pozostanie. Gdy rozmienimy dziesiątkę otrzymamy łącznie 12 jedności do podziału (10 z rozmieniania i 2 wcześniejsze), czyli po 4 jedności dla każdego. To tylko przykładowa kolejność, ale widać, że jeśli zabierzemy się do pracy “byle jak”, to każdym rodzajem znaczków zajmujemy się kilka razy, a odczytanie wyniku wymaga uporządkowania i zamiany znaczków. Gdy spróbujemy zrobić to w kolejności “od lewej do prawej”, uzyskamy wynik w uporządkowanej formie: rozmienimy setkę (uzyskamy 10 dziesiątek, plus 5 które “już były”), rozdzielimy dziesiątki po 5 dla każdego pionka, a następnie jedności po 2 dla każdego pionka. Wynik widać od razu: jest to 52. U pozostałych dzieci, które nie mają potrzeby rozumienia zasad procesu tak dogłębnie, można ten etap pominąć i przejść do prezentacji dzielenia w ogólnej formie.
Dzielenie krok po kroku
Jeśli wykonujemy dzielenie od lewej do prawej i skupiamy się na jednej pozycji dziesiętnej (jednym rodzaju znaczków), to okazuje się, że proces jest prosty, powtarzalny i… intuicyjny! Osoby, które pierwszy raz widzą pracę z montessoriańskim laboratorium, są tym nieraz mocno zaskoczone.

Jak więc wyglądają kolejne kroki?
- bierzemy znaczki o “największym nominale” spośród tych, które nie zostały jeszcze rozdzielone,
- rozdzielamy je po równo między pionki,
- pozostałe znaczki rozmieniamy – każdy na 10 znaczków kolejnego rodzaju,
- i… znów od początku, dopóki nie dojdziemy do jedności.
Tutaj jeden szczegół, który odróżnia pracę na laboratorium od znaczków: po drugim kroku musimy zapisać odpowiednią cyfrę do wyniku (jest to liczba, którą dostał każdy z pionków) i sprzątnąć koraliki z tabliczki.
A co z tym zapisem?
Zapis również może być prosty i intuicyjny – zwykle największy kłopot sprawia dzieciom pracującym z pomocą równe zapisywanie cyfr jedna pod drugą, sam zapis nie sprawia dużych trudności (choć te też mogą się pojawić – szczególnie u dzieci z trudnościami w nauce, ponieważ proces jest dość złożony i zapisujemy cyfry w kilku różnych miejscach).
Najlepiej pokazywać zapis prawie od samego początku. Gdy tylko dziecko zrozumie sam proces dzielenia, możemy zaprezentować mu zapis wykonywanego działania. Warto przy tym kierować się pytaniami, które wskazują, jakie liczby powinniśmy zapisać w trakcie dzielenia. Jakie to pytania?
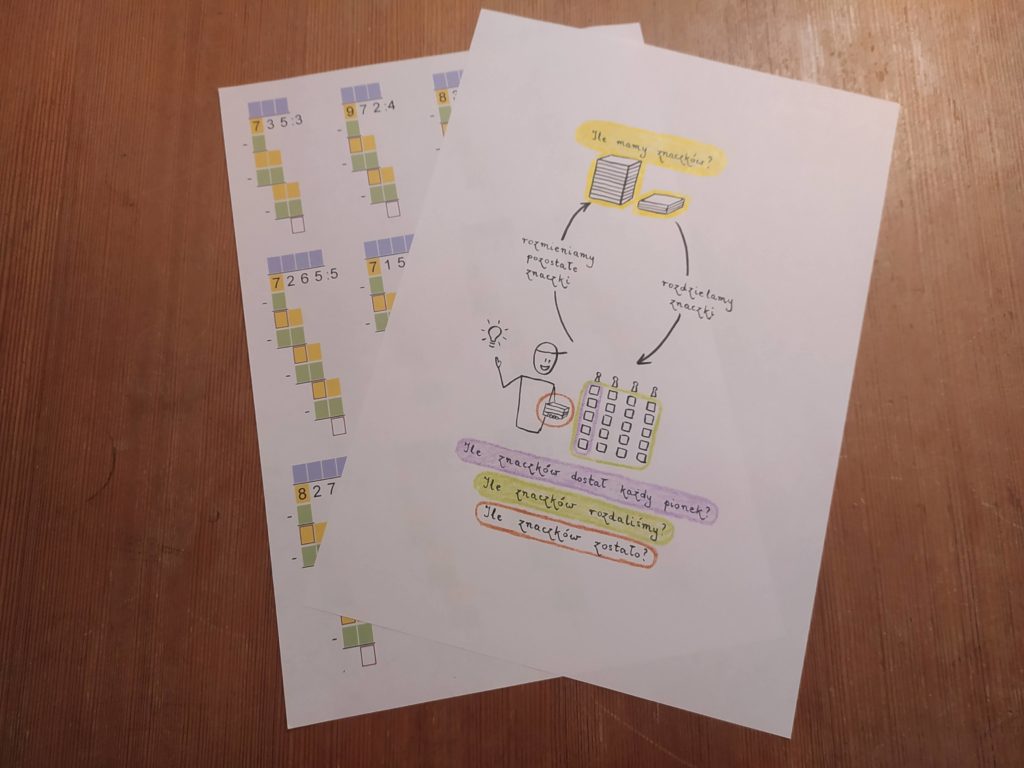
- Ile mamy znaczków? Za pierwszym razem wskazujemy na znaczki o największym “nominale”, natomiast później zadajemy to pytanie zaraz po rozmienianiu: liczba naszych znaczków powstaje przez dodanie znaczków “które były na początku” do tych “z rozmieniania”, to dlatego to pytanie towarzyszy “spisywaniu” kolejnej cyfry z dzielnej.
To moment na to, by rozdzielić te znaczki. Wówczas możemy odpowiedzieć na kolejne pytania:
- Ile dostał każdy pionek? To kolejna cyfra wyniku – piszemy ją na górze, nad dzielną.
- Ile znaczków rozdaliśmy? To znaczki, które już do nas nie wrócą, tę liczbę zapisujemy pod tym ile znaczków mieliśmy, bo to pozwala nam obliczyć…
- Ile znaczków nam zostało? Zapisujemy to jako wynik odejmowania “pod kreską”, dlatego w zapisie dzielenia pojawiają się minusy i dodatkowe kreski. Warto zaznaczyć, że jeśli odpowiedzią na to pytanie jest zero, zamiast symbolu 0 możemy użyć znaku =. Nie jest to znak równości, ale dwie kreski. Dzięki temu zapis odpowiedzi na kolejne pytanie będzie mniej mylący (bez cyfry zero na początku). Jeśli jednak jest to dla dziecka mylące, możemy pozostać przy cyfrze 0.
Te ostatnie znaczki rozmienianiamy i… możemy zadawać pytania od początku 🙂
Zebrane pytania znajdziecie w pliku do pobrania, w wersji do znaczków lub oryginalnego laboratorium.
Z doświadczenia wiem, że na początku dzieci mają problem z równym zapisem tak wielu liczb jedna pod drugą. Dlatego proponuję zaczynać od przykładów z “kratkami”. Ja dodatkowo przygotowałam pytania w kolorach odpowiadających kolorom kratek. Dzięki temu dziecko wie, w którym miejscu wpisać odpowiedzi na poszczególne pytania. Jak zwykle gotowe zadania znajdziecie w Bazach. Opisuję je bardziej szczegółowo niżej.
Gdy zapis “z kratkami” jest już jasny i zrozumiały, zachęcamy dziecko do samodzielnego zapisu – na początkowym etapie warto nadal pozostawić pytania w zasięgu wzroku.
Jakie wyzwania nas czekają?
Jak zwykle na początku proponujemy dziecku takie przykłady, w których proces dzielenia wygląda podobnie na każdym etapie i nie pojawiają się żadne wątpliwości. Takie przykłady zgromadziłam w bazie 30 (tutaj są już “kratki” – przygotowany zapis) i bazie 31 (do samodzielnego zapisu).
Kolejne dwie bazy zawierają różne trudności. Zebrałam je poniżej, żebyśmy mogli towarzyszyć w nich dzieciom.
Dla niektórych dzieci trudność może stanowić też cyfra 0 pojawiająca się w dzielnej. Na etapie abstrakcyjnego dzielenia postępujemy z nią tak samo jak z każdą inną cyfrą. Na etapie pracy z pomocą może pojawić się moment zawahania: zwykle do znaczków z “rozmieniania” dokładamy “te, które już były”. Tym razem ich nie ma, ale to nie szkodzi (cześć dzieci nawet nie zauważa, że mogłaby mieć problem)! Działamy dalej tak jak zwykle.
Kolejna niewielka trudność, pojawia się, gdy w trakcie procesu dzielenia uda nam się podzielić bez reszty (na pytanie “ile znaczków zostało?” odpowiedzią jest 0. Doświadczaliśmy już tego na samym końcu dzielenia. Tym razem zaskakujące może być to, że nie mamy nic do rozmienienia. W takiej sytuacji po prostu sięgamy po kolejny rodzaj znaczków.
Zdecydowanie największy kłopot sprawiają momenty, gdy w trakcie dzielenia doświadczamy, że nie starczy nam znaczków do obdzielenia pionków. Co wtedy? Zapisujemy w wyniku 0 (bo każdy pionek nic nie dostał!), chyba że jest to sam początek dzielenia. O tym zerze łatwo zapomnieć, warto się pilnować! A potem pomijamy kolejne dwa pytania (“bo one nic nie zmienią” jak mówią dzieci) i bierzemy się za rozmienianie. Na początku (albo i na zawsze ;)) możemy nie opuszczać tych pytań i notować odejmowanie zera. Pisania będzie więcej, ale za to więcej powtarzalności i spokoju ducha u niektórych 😉
Na sam koniec zostawiłam resztę z dzielenia, która może pojawić się na końcu. To nic strasznego – tak już z dzieleniem jest, że ta reszta czasem zostaje i nie należy się tego bać. W przygotowanych do tej pory bazach nie ma przykładów z resztą. Dzięki temu jej brak jest częściową kontrolą błędu. Ale przykłady, w których wychodzi czasem reszta, bardzo łatwo uzyskać! Po prostu wylosujcie dzielną i dzielnik, na przykład za pomocą kostek 🙂
Co dalej?
Podobnie jak przy dzieleniu małych liczb, możemy zastanawiać się, czy resztę można również jakoś rozdzielić. W zależności od tego, w jaki sposób to zrobimy, otrzymamy ułamki zwykłe lub dziesiętne. To doskonały sposób, by zacząć je odkrywać!
Oczywiście przed nami również temat dzielenia przez liczby kilkucyfrowe. Tym też się zajmiemy!
A przede wszystkim… mamy już komplet działań na wielkich liczbach! Aż kusi, żeby zacząć ich używać. Zadania nasuwają się same, wystarczy zajrzeć do atlasu lub książki o kosmosie 😉





