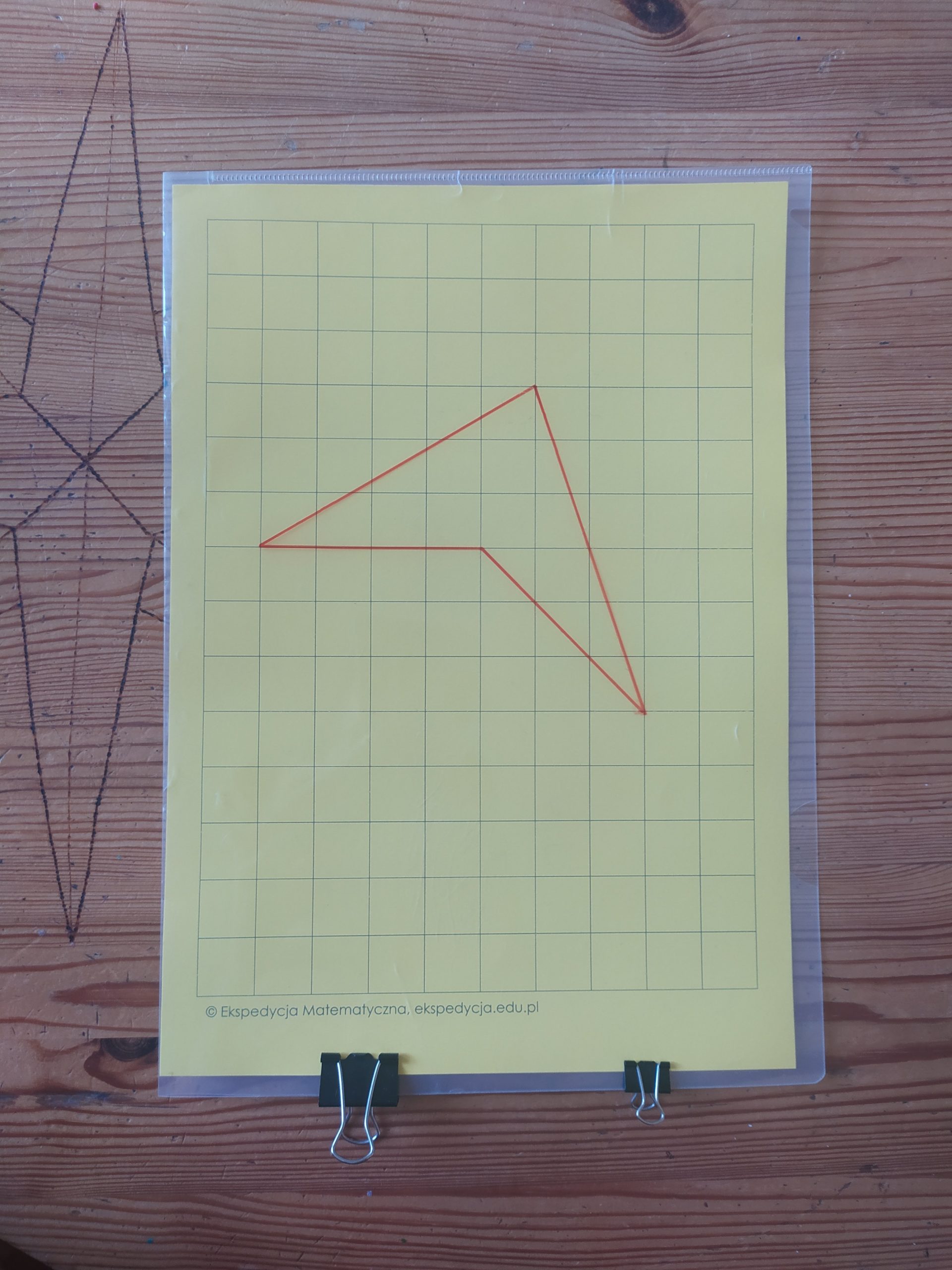
Gdybyśmy mieli kartkę w kratkę i wycięli wielokąt, taki o wierzchołkach na przecięciach kratek… Jak najłatwiej obliczyć jego pole?
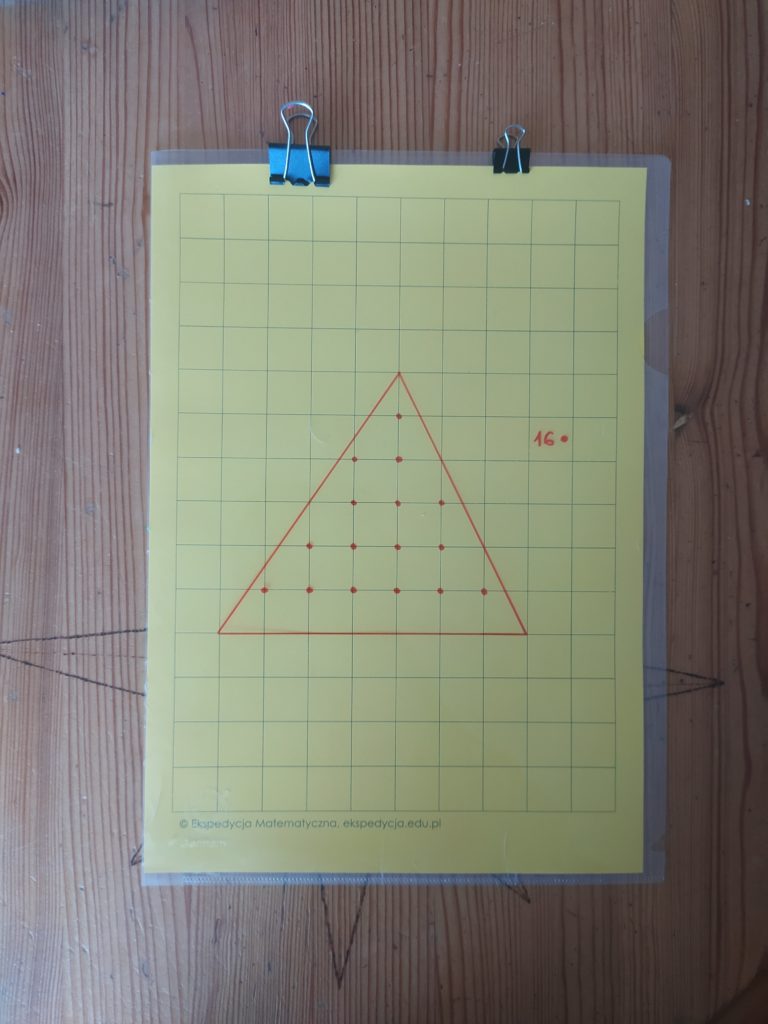
Spróbujmy najpierw z trójkątem, podobnym do tego z pudełka pól. Jego pole możemy łatwo obliczyć dzięki wzorowi na pole trójkąta, albo tnąc go i układając prostokąt. Ile wyszło? 21 kratek 🙂
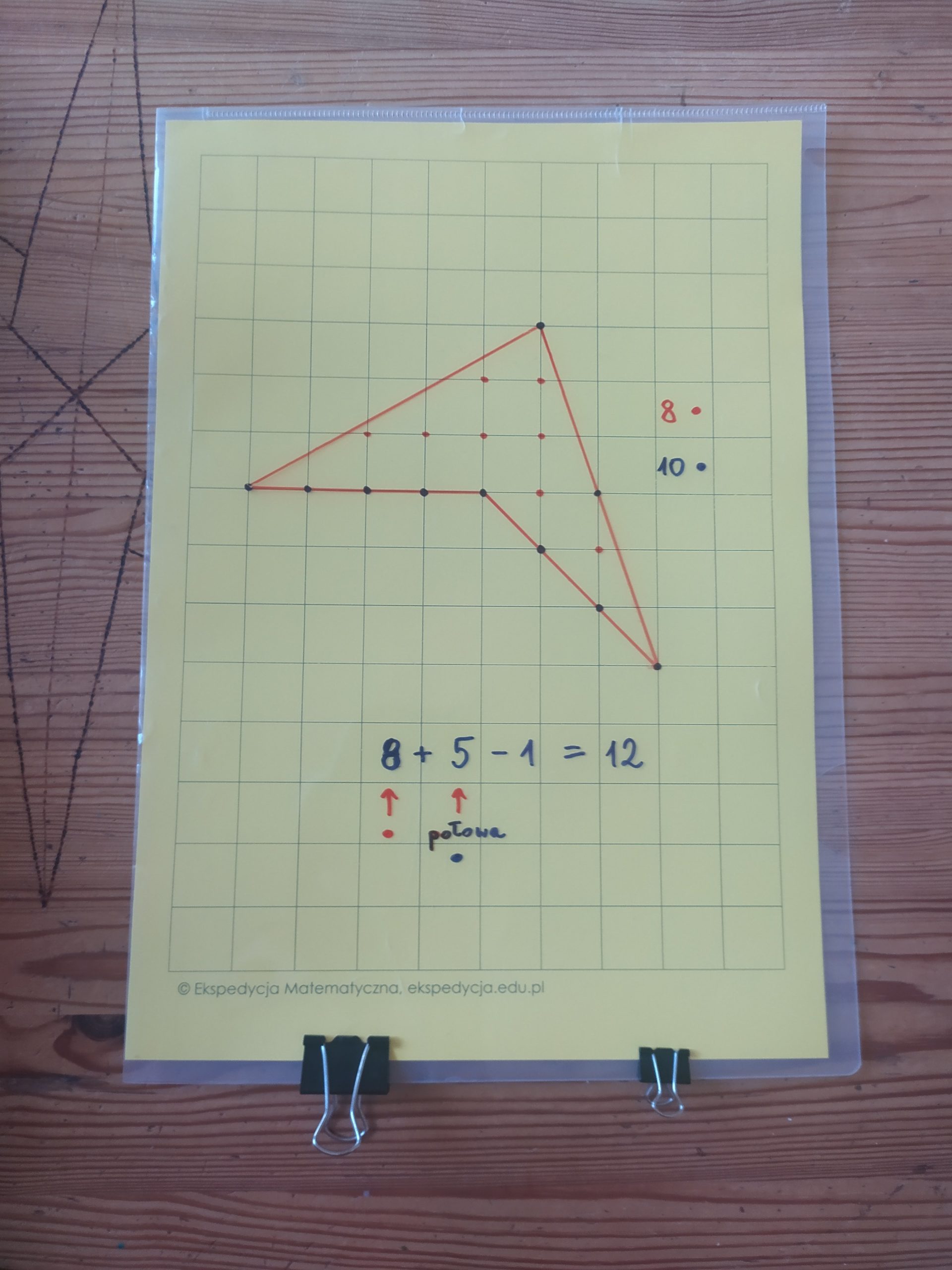
A czy można inaczej? Dziś Dzień Kropki, więc spróbujemy policzyć kropki ☺️ Na początek postawimy czerwoną kropkę na każdym “skrzyżowaniu” kratek, które wypada wewnątrz naszej figury. Takich kropek jest 16.
Teraz liczymy te kropki, które wypadają na brzegu naszej figury (również w wierzchołkach), ale z nich bierzemy tylko połowę. U nas takich granatowych kropek jest 12, połowa to 6. Na koniec dodajemy, odejmujemy 1 i…
16+6-1=21 – tyle samo co pole… Czy to przypadek?
Okazuje się, że to nie przypadek! Tak jest w każdym wielokącie “bez dziur”, który ma wierzchołki w skrzyżowaniach kratek. Ten wzór nosi nazwę wzoru Picka.
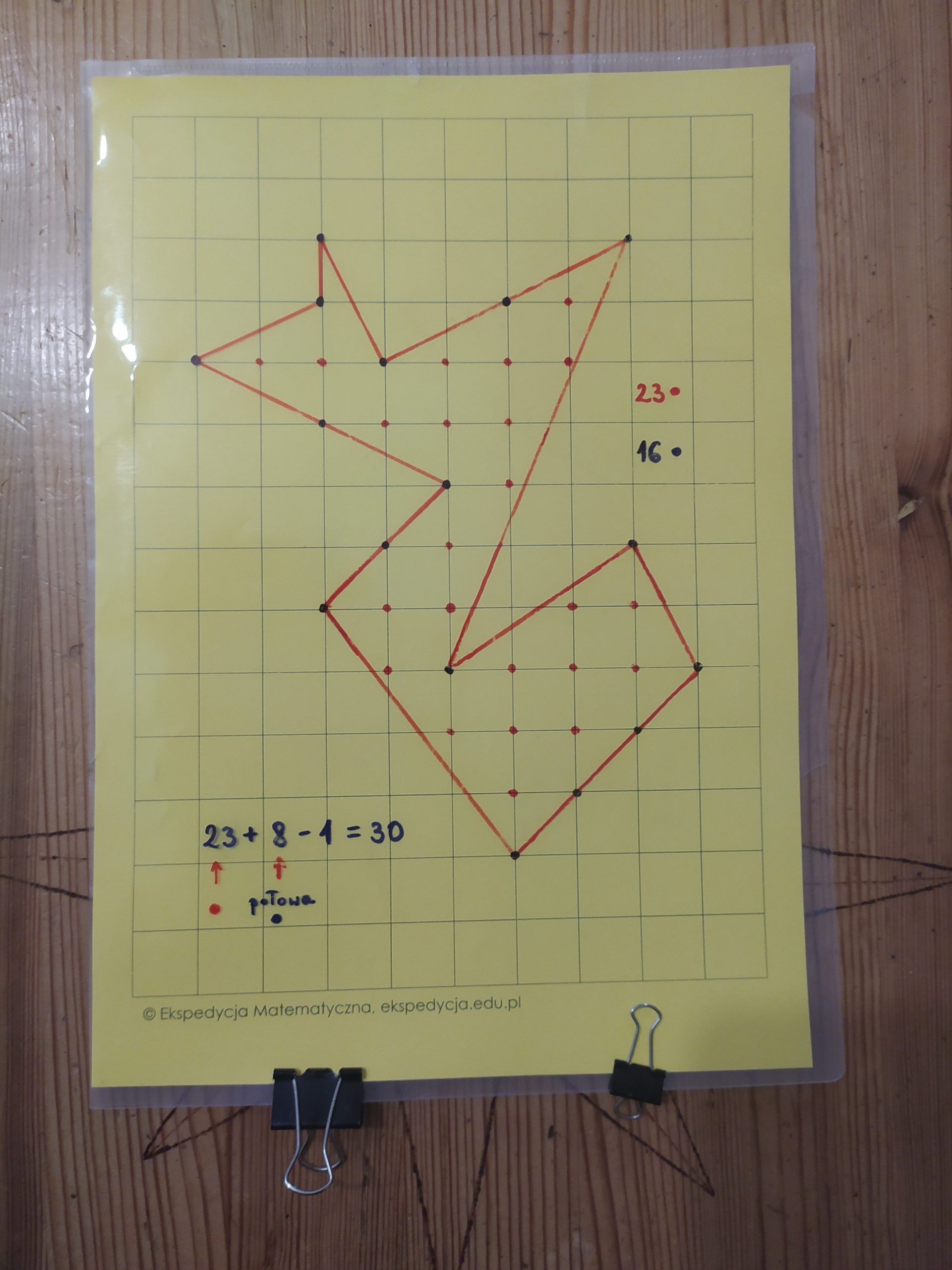
Jeśli nie dowierzacie, że to działa, koniecznie spróbujcie na innych figurach! Ja wybrałam jeszcze dwie, przy których trzeba “szkolnymi metodami” trochę się natrudzić. Spróbujcie obłożyć ich pola i porównać z wynikami, które otrzymałam z wzoru Picka. Może też pomogą wam zrozumieć, jak stosować ten wzór 🤗
No dobrze, śmieszny wzór, a zamiast kwadratów liczymy kropki, ale… dlaczego to działa???
Spróbuję wam pokazać, dlaczego to może działać. Nie będzie to dowód, a jedynie pewna intuicja. Zrobię to na rysunku z pierwszym trójkątem, ale przy innych wielokątach wypukłych będzie to wyglądało podobnie. Przy wklęsłych trzeba się chwilę dłużej zastanowić, a po prawdziwy dowód… Cóż, jestem przekonana, że zainteresowani znajdą go bez problemu 😁
Zaczniemy od przesunięcia naszych kratek (to dlatego od początku kratki miałam wydrukowane – znajdziecie je poniżej, a figurę i kropki rysowałam na przypiętej folii). Umieścimy je tak, aby kropki znalazły się na środku kwadratów.
-
 Papier w kratkę do badania pól0,00 zł
Papier w kratkę do badania pól0,00 zł

Teraz wokół każdej czerwonej kropki rysuję czerwony kwadrat, który wliczę do pola. Wokół granatowych kropek rysuję połowę kwadratu – wybieram taką “uciętą wzdłuż boku figury”. Powstała nam prawie nasza figura, tylko… “w minecraftowej wersji”, jak określiły to moje dzieci. Czy ma takie samo pole jak wyjściowa figura?
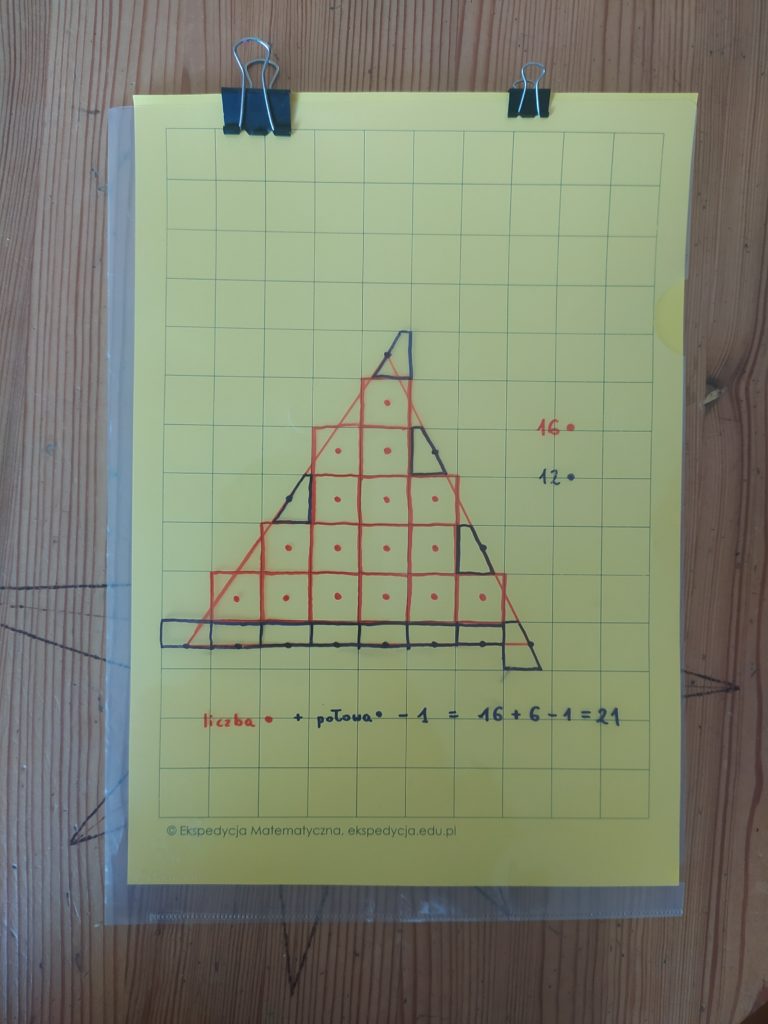
Widać, że część czerwonych kwadratów “wystaje” poza figurę, za to niektóre kawałki figury są niezakryte. Okazuje się jednak, że te “nadmiarowe” kawałki idealnie pasują do “dziur” (to ten moment, który formalnym dowodem nie jest). A granatowe połówki kwadratów? Trochę wystają przy wierzchołkach naszej figury. Musimy się tych wystających kawałków pozbyć. Okazuje się, że one razem tworzą jedną kratkę. Jeśli nie wierzysz, przyjrzyj się im ☺️ Najłatwiej stwierdzić to wiedząc, że suma kątów zewnętrznych każdego wielokąta jest równa 360 stopni.
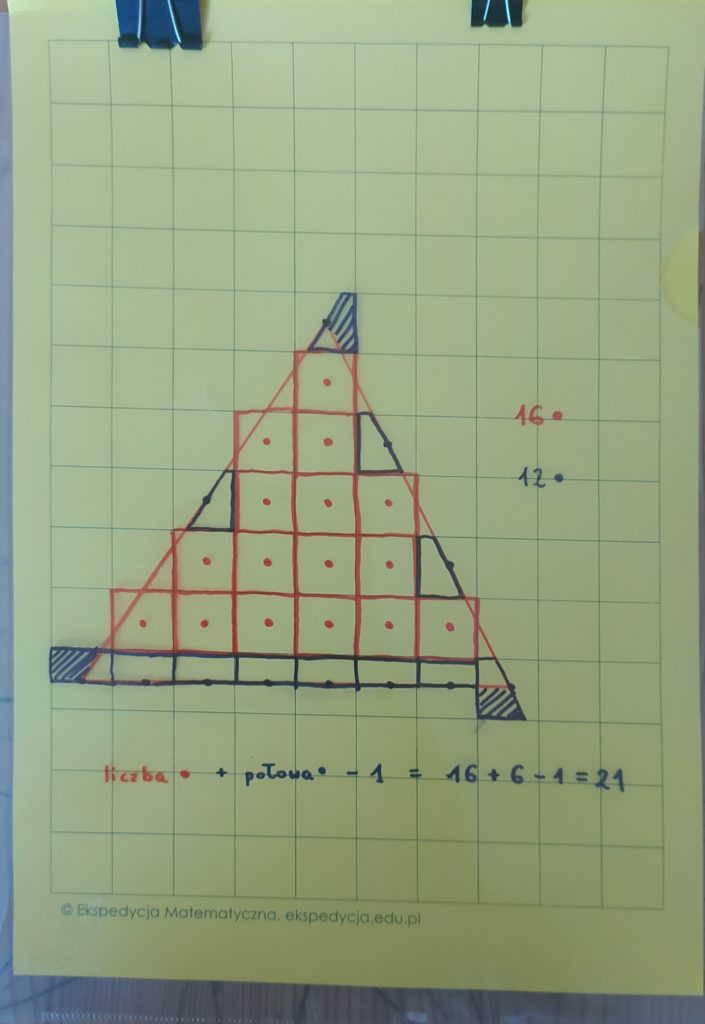
To jak, czujecie się przekonani? Będziecie liczyć pole metodą kropek? Zróbcie to chociaż dziś, żeby uczcić kropki, a samemu zobaczyć, jak zaskakująca jest matematyka 😀