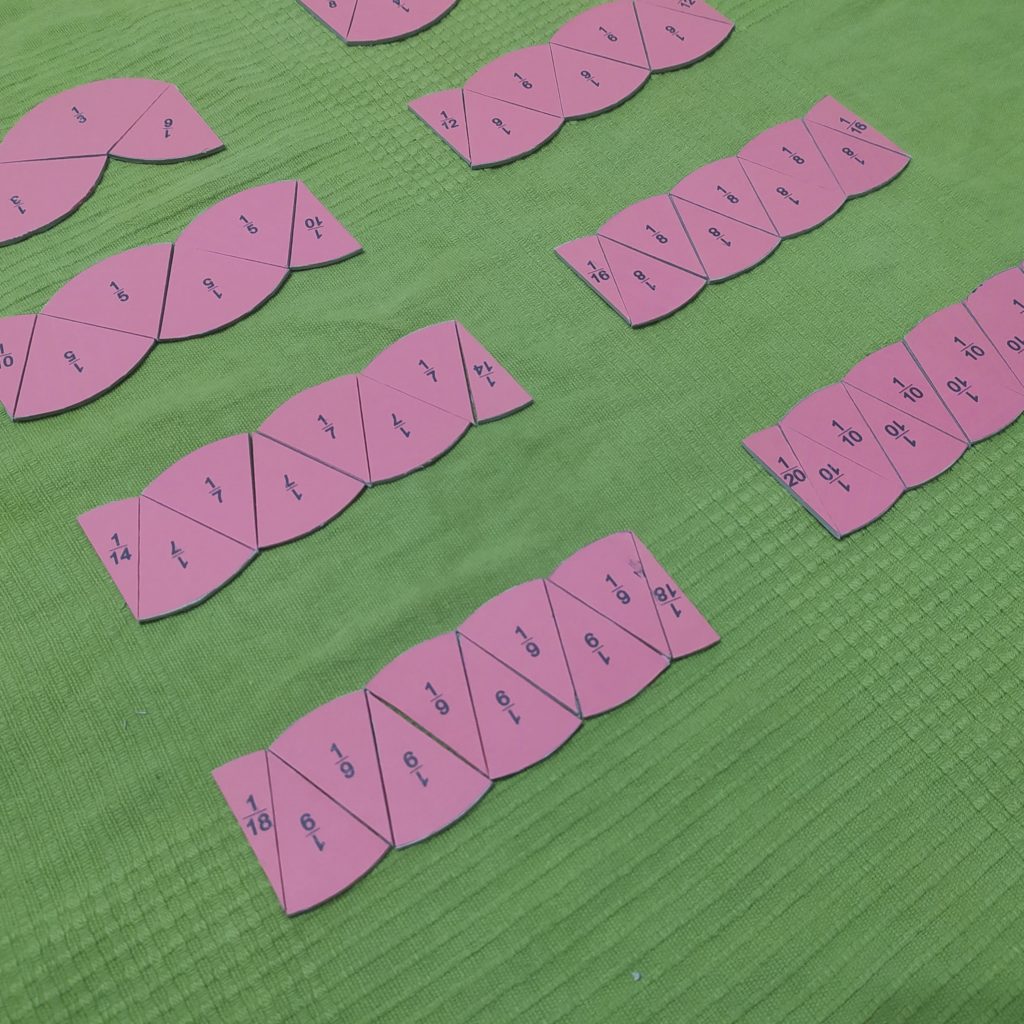Dziś dzień liczby π 🙂 W zeszłym roku pisałam o przybliżaniu liczby π – wystarczy przecież zmierzyć średnicę i obwód koła, podzielić drugie przez pierwsze i mamy pewne przybliżenie 🙂
Dziś chciałabym pokazać, jak montessoriańskie ułamki (które możecie wykonać samodzielnie) mogą przydać się do okrycia wzoru na pole koła.
-
 Ułamki zwykłe0,00 zł
Ułamki zwykłe0,00 zł
Spróbujmy jednostkowe koło z ułamków podzielić na jednakowe części. Ułożyłam jedno koło z części trzecich, jedno koło z części czwartych i… tak aż do części dziesiątych.

Teraz w każdym z kół jedną z części wymieniłam na dwie jednakowe. O tak:
Teraz każde z kół zamieniłam w pewną figurę o dość fantazyjnym kształcie. W jaki sposób? Zaczęłam od “mniejszej” części, potem dołożyłam “większe” (są obrócone na dwa sposoby, na zmianę), a na koniec drugą “mniejszą” część. Zdjęcia najlepiej to wyjaśnią 🙂
Co możemy powiedzieć o powstałych figurach? Każda z nich ma takie samo pole, jak koło jedności. A do tego… te figury coraz bardziej przypominają pewien prostokąt! Skoro tak, to ten (jeszcze niewidzialny) prostokąt też będzie miał takie pole, jak nasze koło!

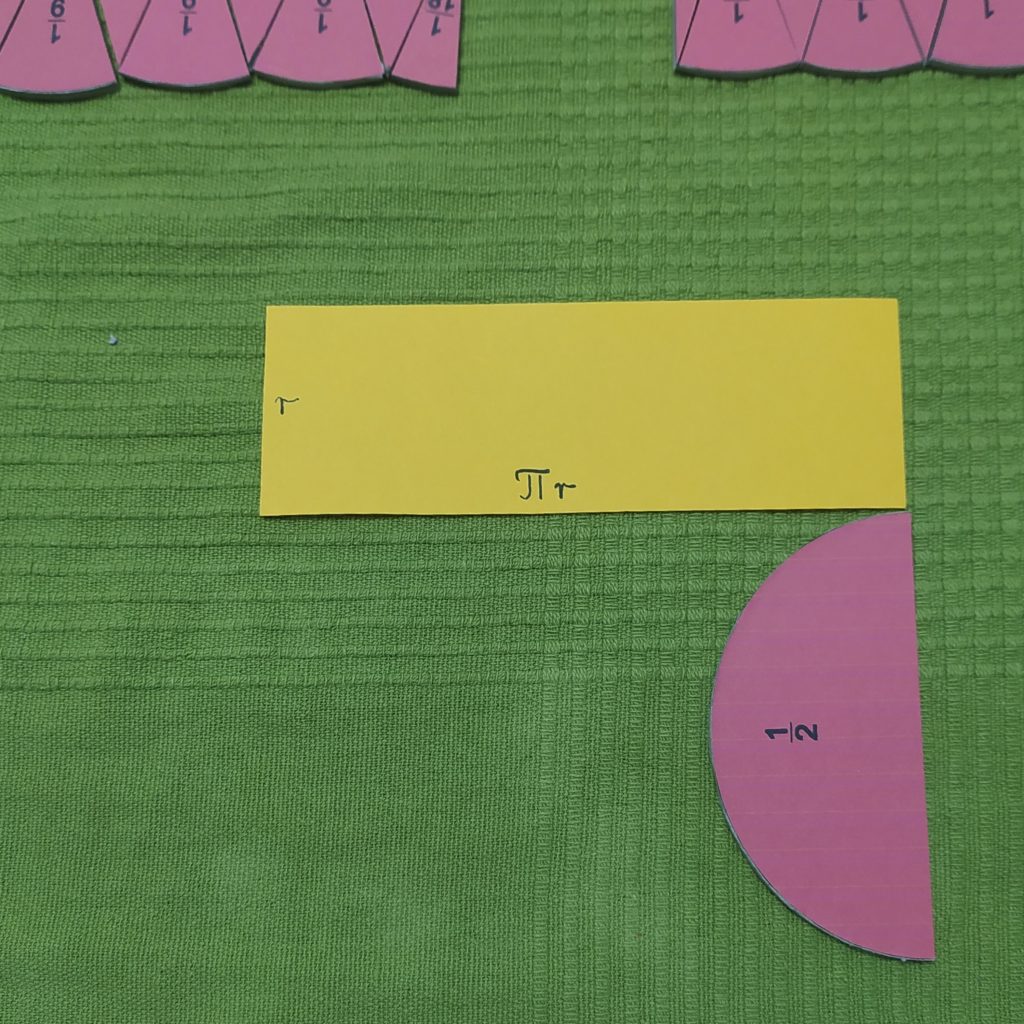
Spróbujmy się przyjrzeć, co to za prostokąt? Jego “pionowy” bok, szerokość, to po prostu promień naszego koła (widać ten promień doskonale z lewej i prawej strony każdej figury). A “poziomy” bok, szerokość? Dwie krzywe, które ograniczają nasze figury od góry i od dołu, są takie same. A ponadto ich fragmenty po złożeniu ułamków w koło, tworzą obwód tego koła! To oznacza, że długość prostokąta jest taka sama, jak pół obwodu naszego koła.
Możemy tego doświadczyć również “przetaczając” pół koła (czyli jedną drugą!) po dłuższym boku naszego prostokąta.
To jakie jest w końcu pole koła? Takie samo, jak pole naszego prostokąta. Aby je obliczyć, musimy pomnożyć szerokość przez długość: r·πr. Kto ma doświadczenie z wyrażeniami algebraicznymi, zaraz przekształci to do tradycyjnej postaci πr2.