Od wielokątów foremnych po wyprawę dookoła świata

Dziś chciałabym pokazać coś, co nie mieści się (a przynajmniej nie w pełni) w podstawie programowej. Nie wymaga też dużej wiedzy matematycznej (ot, liczenie w zakresie sześciu i nazwy wielokątów, a nawet to nie jest niezbędne). Pokazuje za to sens matematyki. W zasadzie dwa różne sensy – piękno samo w sobie (uwielbiam zachwyt nad matematyką, a jeszcze bardziej jego wywoływanie u uczniów!) i zastosowanie do rzeczywistych problemów.

Na początku były wielokąty… 😉

Historia zaczyna się niepozornie, od wielokątów foremnych. Niby proste, ale potrafią zaskoczyć. Jeśli chcecie, przygotujcie sobie wielokąty foremne, na przykład z tektury (idealna jest tektura introligatorska). Oczywiście świetnie nadadzą się też takie z różnych układanek. Najlepiej, jeśli wszystkie wielokąty mają boki tej samej długości. Możecie pobrać wzory wielokątów z przygotowanego pliku 🙂 wystarczy wam 7 trójkątów, 5 czworokątów i po 4 pięciokąty, sześciokąty i siedmiokąty. Jeśli chcecie, zróbcie ich więcej, możecie też przygotować ośmiokąty.

Na początku, jeśli dziecko nie ma takich doświadczeń, warto pozwolić mu na układanie figur na płaszczyźnie – na przykład na biurku. Powiedzmy też o tym, co wyjątkowego jest w wielokątach foremnych – są niezwykle regularne, mają boku jednakowej długości, również ich kąty są takie same. Dopiero po takim etapie swobodnej zabawy zabieramy dziecko na podróż w trzeci wymiar 🙂

Wielościany

Teraz pora na budowanie wielościanów z naszych wielokątów. Niestety technicznie jest to dość trudne. Najlepiej będzie wziąć w tym celu mocną taśmę i sklejać wielokąty wzdłuż boków. Można oczywiście spróbować również składać wielościany z siatki lub budować z patyczków, ale to nie pozwoli dzieciom doświadczyć tej rzeczy, o której akurat teraz chcę napisać.

Powiedzmy dziecku, że będziemy chcieli zbudować wielościany foremne. Każdy z nich będzie zbudowany z jednakowych wielokątów foremnych w taki sposób, żeby w każdym wierzchołku “spotkało” się ich tyle samo. Dodatkowo będziemy chcieli, żeby nasza bryła była wypukła – przy budowaniu brył będzie to naturalne, ponieważ nie jesteśmy w stanie zrealizować przecinania się ścian. Osoby zainteresowane tym tematem odsyłam do bardzo dobrego artykułu w czasopiśmie “Delta”.

Wybierzmy z dzieckiem jeden z dostępnych kształtów – trójkąt, czworokąt, pięciokąt, sześciokąt, a może siedmiokąt? Spróbujmy na początek skleić jeden narożnik – tu warto dodać, że nie musi to jeszcze nieść sukcesu w postaci całej bryły, ale akurat przy wielościanach foremnych nie będzie z tym problemu. Warunek, o którym możemy powiedzieć dziecku, to że nie chcemy by w jednym wierzchołku wielokąty schodziły się nieregularnie, “w harmonijkę”.

Niezależnie od wybranego kształtu, nie uda nam się uzyskać wierzchołka bryły za pomocą jednego lub dwóch wielokątów. Dwa będą do siebie przylegać, a przecież “między nimi” miało być wnętrze bryły.

Jeśli wybraliśmy trójkąty, spróbujmy je ze sobą łączyć. Możemy połączyć trzy trójkąty w jednym narożniku (gdy spróbujemy dokończyć taką bryłę, otrzymamy czworościan, ale to sprawdzimy za chwilę), cztery trójkąty (robiąc to samo w pozostałych wierzchołkach otrzymamy ośmiościan), pięć trójkątów (tutaj dokończenie wymaga więcej pracy, ale uda się! otrzymamy dwudziestościan), a sześć trójkątów… rozłoży się na płasko. Większa liczba trójkątów wymagałaby złożenia ich “w harmonijkę” i nie dałaby  wypukłego wierzchołka.

Przy wyborze czworokątów (kwadratów) możliwości nie ma aż tyle. Połączenie trzech kwadratów w  wierzchołku pozwoli nam na uzyskanie sześcianu. Cztery kwadraty rozłożą się “płasko” i nie dadzą skończonej bryły, a większa ich liczba wyklucza wypukłość. Stąd jedynym wielościanem foremnym złożonym z kwadratów będzie sześcian.

Jeśli zaczniemy od pięciokątów, możemy połączyć w wypukły sposób tylko trzy pięciokąty – z takich narożników uda nam się złożyć dwunastościan.

Z sześciokątów nie uda nam się złożyć wypukłego wierzchołka, ponieważ już trzy sześciokąty rozkładają się “na płasko”. Jeszcze gorzej jest z siedmiokątami (i wszystkimi kolejnymi wielokątami foremnymi) – ich nawet na płasko nie uda się złożyć…

W takim razie to już wszystkie! Nie tylko znaleźliśmy pięć wielościanów foremnych, ale też mamy pewność, że żadnych innych być nie może.

Jak zrobić takie bryły w całości?

Można próbować sklejać całe bryły, ale nie jest to łatwe. Również budowanie ich z siatek jest mozolne, szczególnie w przypadku dwunastościanu i dwudziestościanu. Chciałabym pokazać wam jeszcze jeden sposób, w którym dzieci mogą zdziałać najwięcej samodzielnie 🙂

Potrzebne do tego będą koła opisane na wielokątach foremnych. Odrysowujemy na nich wielokąt i nacinamy każdy bok do połowy. Jeśli chcesz, narysowane koła możesz wydrukować z gotowego pliku w wersji czarno-białej lub kolorowej.

Nacięcia tak przygotowanych kół nasuwamy jedno w drugie, łącząc w ten sposób wielokąty wzdłuż boków. Łącząc odpowiednie liczby kół w każdym wierzchołku uzyskamy nasze wielościany – spróbujcie!

Na dwudziestościan, który jest najbardziej skomplikowany, jest jeszcze jeden cudowny i zaskakujący sposób 🙂

Potrzebne nam będą “paski”, każdy złożony z 10 trójkątów równobocznych i jedenastego (lub jego kawałka) do sklejenia. Możecie pobrać gotowy wzór z pliku. Potrzebne będą cztery paski, a najlepiej sześć (wówczas bryła jest stabilniejsza). Wycinamy je i każdy sklejamy “w kółko”.

Teraz wystarczy nasunąć takie kółka na siebie i już! Prawda, że cudowne?

A po co nam to wszystko?

Wielościany foremne są piękne i regularne, ale nie spotkamy ich zbyt często (przynajmniej dwunastościanu czy dwudziestościanu). Można poszukać inspiracji nimi w architekturze. Dziś jednak chciałabym pokazać wam inne, niebanalne wykorzystanie dwudziestościanu.

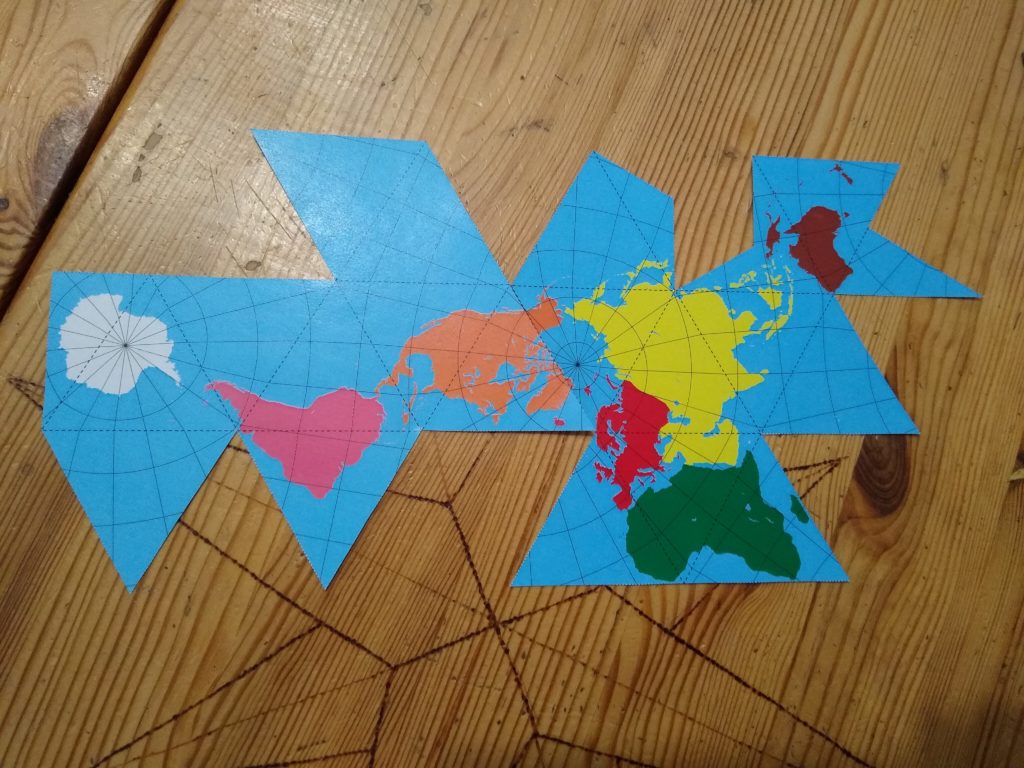
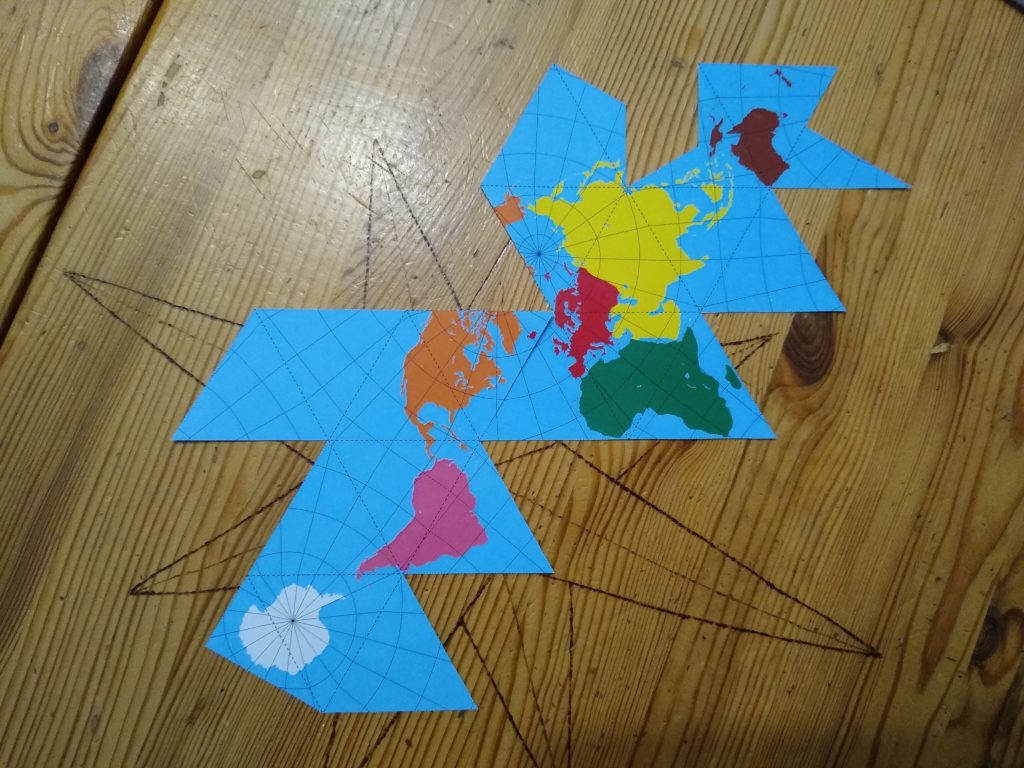
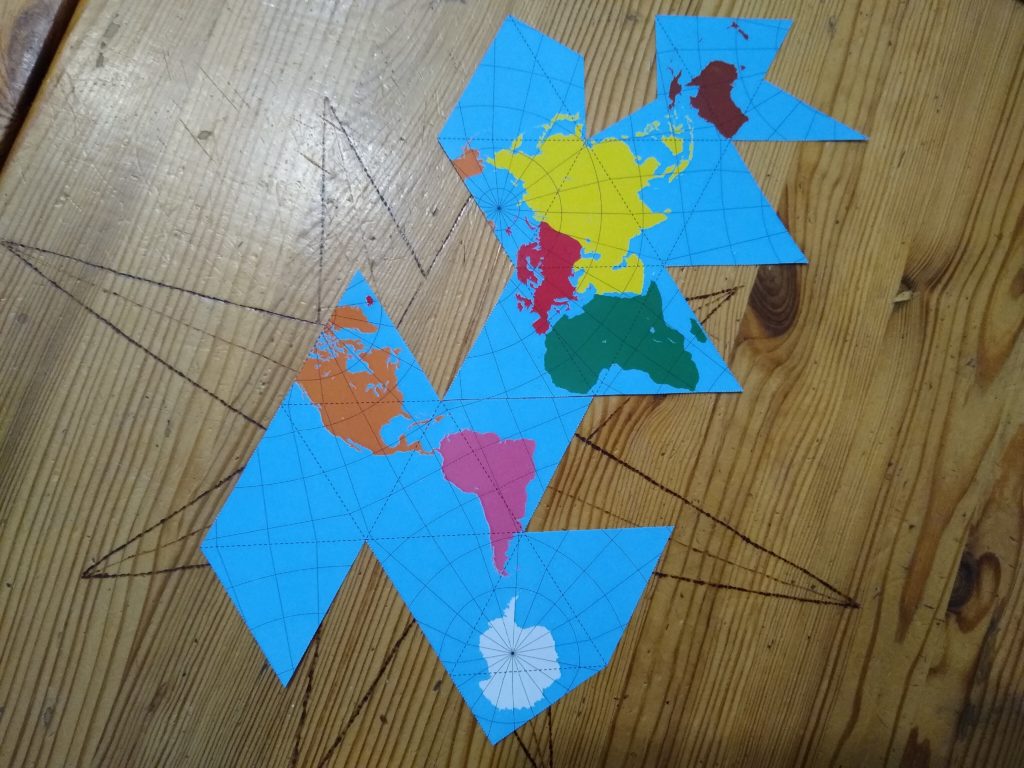
Kolejne (przy uporządkowaniu pod względem liczby ścian) wielościany foremne coraz bardziej przypominają kulę. I co z tego? Ano to, że możemy spróbować na dwudziestościanie odwzorować kulę ziemską. Chcecie zobaczyć? Możecie pobrać go, wyciąć i nakleić na złożony z pasków dwudziestościan 🙂 Można też wydrukować go na tekturze i skleić (to będzie wymagać dorobienia odpowiednich zakładek do przyklejenia) lub wykonać dwudziestościan (długość krawędzi to ok. 53mm) z twardej tektury i nakleić na niego mapę. A jeśli chcecie większy rozmiar, to znajdziecie również większe rozmiary 🙂

• 

• 

Jak każde przybliżenie, na swoje plusy i minusy. Niewątpliwie zalet jest wiele:

• stosunkowo dobrze oddaje wielkości (odległości i powierzchnię) – na tradycyjnych przedstawieniach całej kuli ziemskiej zwykle w okolicach bieguna wszystko jest mocno powiększone,
• linie “podziału” przy rozkładaniu nie rozcinają żadnego lądu (nie było to łatwe! wymagało rozcięcia dwóch ścian),
• pozwala doskonale prześledzić kolonizację świata przez ludzi pierwotnych – od Afryki po Australię,
• założona na dwudziestościan z pasków jest świetnym zastępnikiem globusa, otrzymanym w 10-15 minut,
• wyciąga nas z naszych przyzwyczajeń 😀 i pozwala na nowo wziąć się za wędrówki palcem po mapie 🙂

Co więcej, siatką można stosunkowo łatwo manipulować przy odrobinie wyobraźni przestrzennej. Gdybyśmy chcieli otrzymać mapę, na której ocean między Afryką i Amerykami jest w całości, wystarczy ją rozciąć i odpowiednio przyłożyć otrzymane części 🙂 Spróbujcie koniecznie!

• 

• 

• 

• 

A minusy?

• przede wszystkim linie ułatwiające nawigację (położone pod stałym kątem względem linii północ-południe) nie są na niej liniami prostymi tak jak na mapie Merkatora.

Jeśli więc wypływacie statkiem w podróż dookoła świata, zabierzcie ze sobą raczej inną mapę, a tę zachowajcie sobie do celów edukacyjnych 😉