Co to są te liczby pierwsze? To takie, które dzielą się tylko przez 1 i samą siebie. Liczby złożone to takie, które mają więcej niż dwa dzielniki. Tyle mamy suchej definicji, która jest na tyle abstrakcyjna, że nie wyjaśnia ani powodu, ani celu ich używania. Warto więc zacząć rozmowę o liczbach pierwszych i złożonych od pewnej opowieści… Liczby pierwsze to takie cegiełki, z których za pomocą mnożenia możemy uzyskać każdą liczbę, i to na jeden wyjątkowy sposób. Możemy to trochę porównać do układania liczb z jedynek za pomocą dodawania – tyle, że tym razem różnych cegiełek jest więcej niż jedna (jest ich nawet nieskończenie wiele).
Po takim wstępie możemy zabrać się do poszukiwania liczb pierwszych. Jedyne, co musimy wiedzieć, by rozpocząć przygodę, to pojęcie wielokrotności i dzielnika (o sposobie ich wprowadzania możecie przeczytać w poprzednim wpisie). Proponuję najpierw sprawdzić z dzieckiem, które z liczb od 1 do 10 są pierwsze, a które złożone. Co ważne, liczba 1 jako jedyna liczba naturalna nie jest ani pierwsza, ani złożona, ponieważ jako jedyna ma tylko jeden dzielnik (jest to 1). Do tego jeszcze wrócimy, gdy lepiej zrozumiemy liczby pierwsze (we wpisie o rozkładzie na czynniki pierwsze), ale warto liczbę jeden od razu “odrzucić” z naszego podziału.
Dla każdej z liczb od 2 do 10 wypiszmy z dzieckiem jej dzielniki. Jeśli mamy z tym problem, możemy skorzystać na przykład z kolorowych liczb i układania prostokątów. Możemy teraz zauważyć, że każda z liczb dzieli się przez 1 i przez siebie. Ale niektóre (4, 6, 8, 9 i 10) mają też inne dzielniki. To dlatego te liczby są liczbami złożonymi. Pozostałe (2, 3, 5 i 7) to liczby pierwsze. Spróbujmy przyjrzeć się liczbom złożonym i zapisać je w postaci mnożenia odpowiadającego dzielnikom różnym od 1 i samej tej liczby (możemy zrobić to patrząc na ułożone z kolorowych liczb prostokąty). Teraz widać, że wszystkie te liczby złożone, poza 8, są wynikiem mnożenia liczb pierwszych. A co z liczbą 8? Jest to 2×4, a 4 to 2×2, możemy więc zamienić w zapisie 2×4 czwórkę przez 2×2 i otrzymamy 2x2x2. Jest to rozkład liczby osiem na czynniki pierwsze – budowa z cegiełek, o której mówiliśmy. O niej będziemy uczyć się, gdy poznamy więcej liczb pierwszych 🙂

No dobrze, wiemy już czym są liczby pierwsze, ale jak je rozpoznać? Warto spróbować z dzieckiem rozpoznać w przypadku kilku liczb, czy są pierwsze, czy złożone.
- Zacznijmy na przykład od liczby, która pojawia się jako wynik w tabliczce mnożenia (jeśli dziecko nie zna jej jeszcze dobrze, lepiej zacząć od kolejnych przykładów): czy 21 jest liczbą pierwszą? Jeśli dziecko pamięta, że jest to 3×7, możemy wywnioskować, że jest to liczba złożona. I tu możemy wysnuć pierwszy ważny wniosek: jeśli umiemy zapisać liczbę jako iloczyn liczb większych od 1, to na pewno jest to liczba złożona. Nie musimy szukać wszystkich dzielników jakiejś liczby!
- Spróbujmy teraz pokazać jakąś liczbę, która w tabliczce mnożenia się nie pojawia, ale łatwo sprawdzić, przez co się dzieli. Takim przykładem może być liczba 58 – dziecko może rozpoznać, że jest to liczba parzysta, więc dzieli się przez 2. W takim razie możemy wyciągnąć kolejny wniosek: wystarczy nam znajomość tylko jednego dzielnika (nie musimy nawet znać drugiego “z pary”), różnego od 1 i danej liczby. Możemy wówczas stwierdzić, że liczba jest złożona
- Jeśli dziecko zna cechy podzielności, możemy pokusić się o jeszcze jeden podobny przykład, w którym trudniej rozpoznać dzielnik, np. liczbę 51. Ta liczba dzieli się przez 3, ponieważ suma jej cyfr (równa 6) dzieli się przez 3. W takim razie 51 również jest liczbą złożoną.
- Pora na liczbę, w której cechy podzielności nam nie pomogą, na przykład 89 i 91. Dzięki cechom podzielności łatwo możemy stwierdzić, że te liczby nie dzielą się przez 2, 3, 5, 9 czy 10. Ale czy to znaczy, że nie mają żadnych dzielników? Pozwólmy dziecku popróbować, poszukać. Być może sprawdzi liczby 4 lub 6, licząc kolejne wielokrotności. A może zauważy, że ich wielokrotności są parzyste, więc 89 i 91 do nich nie należą 🙂 Może spróbuje liczbę 7. Jeśli zrobi to uważnie, uda mu się odkryć, że wielokrotnością liczby 7 jest 91, więc 91 jest liczbą złożoną. Zagadką nadal pozostaje liczba 89 – może dzieli się przez 11, 12, 13…? Dajmy dziecku czas na zastanowienie się, ale też nie przedłużajmy tego czasu nadmiernie, by nie zniechęcić – zdradźmy, że jest sposób na znalezienie wszystkich liczb pierwszych od 1 do 100, a nawet jakiejś większej, ustalonej liczby.
Sito Eratostenesa
Pomysł ten pochodzi jeszcze ze starożytności i przypisuje się go Eratostenesowi. Nazywane jest sitem Eratostenesa, ponieważ będziemy spośród wszystkich interesujących nas liczb “odsiewać” te złożone, tak długo, aż zostaną nam tylko liczby pierwsze.
Bierzemy tabelę interesujących nas liczb (ja przygotowałam do druku gotową tabelę liczb od 1 do 130) i będziemy z niej wykreślać liczby złożone tak długo, aż zostaną tylko liczby, o których będziemy pewni, że są pierwsze. Jeśli nie korzystacie z gotowej tabeli, polecam zacząć od stworzenia jej z dzieckiem i zaznaczenia (lub po prostu zamalowania) pola z liczbą 1 – ona nie jest ani pierwsza, ani złożona, staramy się to wyraźnie zaznaczyć). Do kolejnych kroków warto przygotować kolorowe pisaki i kolejne etapy wykonywać różnymi kolorami – wówczas lepiej widać opisane zależności. Ja zdecydowałam się na jeden kolor, ale oznaczam wielokrotności poszczególnych liczb, żeby dzieciom było łatwiej śledzić, co się dzieje. Liczby pierwsze umieszczam w zamalowanym kółku. Złożone zamiast skreślać, biorę w kółko, żeby łatwiej było odczytać na zdjęciach, co się dzieje. Jeśli chcecie, użyjcie takich samych oznaczeń.
-
 Tabela do sita Eratostenesa0,00 zł
Tabela do sita Eratostenesa0,00 zł
Możecie zalaminować kartkę z tabelką, możecie wykonywać zaznaczenia bezpośrednio na kartce. Możecie też robić je na folii (ja wykorzystałam rozcięte koszulki foliowe, ale wygodniejsza szczególnie dla dziecka jest sztywniejsza folia). Rozwiązanie z folią może być szczególnie cenne dla dzieciaków, które mają problem w skupieniu się na wielokrotnościach ustalonej liczby, gdy mają zaznaczone już inne – wówczas jest możliwość oddzielenia oznaczeń na czas ich wykonywania, i dopiero późniejsze połączenie. Dodam jeszcze, że jeśli będziecie mieli wątpliwości przy zaznaczaniu wielokrotności poszczególnych liczb, możecie skorzystać z kart kontrolnych.
Popatrzmy teraz na najmniejszą liczbę w tabeli, poza liczbą 1. Jest to 2. Wiemy, że jest to liczba pierwsza – dzieli się tylko przez 1 i przez 2 (więcej “potencjalnych dzielników” po prostu nie ma). Zaznaczmy ją (w inny sposób niż wykreślane wielokrotności, proponuję wziąć ją w kółko). Następnie wykreślamy z tabeli wszystkie dalsze wielokrotności liczby 2 (czyli po prostu liczby parzyste) – one na pewno nie są pierwsze, ponieważ dzielą się przez 2 i są większe od 2. Podkreślam te warunki, ponieważ często zapominamy o drugim warunku i używamy skrótu myślowego, że “liczba parzysta nie może być pierwsza”. Jest to prawda tylko jeśli mówimy o liczbach większych od 2 – liczba 2 jest i parzysta, i pierwsza.

Teraz patrzymy na kolejną liczbę, jest to 3. Ponieważ 3 dzieli się tylko przez 1 i 3 (nie dzieli się przez 2 – nie zostało wykreślone w poprzednim kroku), jest liczbą pierwszą, zaznaczamy je w kółko. Teraz wykreślamy z tabeli wszystkie pozostałe wielokrotności liczby 3. Dziecko może zauważyć, że część tych liczb (na przykład 6 i 12) została wykreślone już wcześniej. Mimo to są też takie liczby, które wykreślamy dopiero teraz, najmniejszą taką liczbą jest 9 (warto to zaznaczyć, będzie to przydatne później!).

Przyszła pora na liczbę 4. Liczba cztery jest już skreślona, więc nie jest liczbą pierwszą, ale musimy wykreślić z tabeli jej wielokrotności (ponieważ są to liczby podzielne przez 4 i większe niż 4, czyli są złożone). No właśnie… czy musimy? Dajmy dziecku spróbować. Powinno szybko zauważyć, że wszystkie wielokrotności liczby 4 są już wykreślone. To właśnie dlatego, że 4 jest liczbą złożoną: dzieli się przez 2, więc każda jej wielokrotność jest też wielokrotnością dwóch i została już wykreślona.
Teraz pora na liczbę 5. Ona również nie dzieli się przez żadną z mniejszych liczb (poza jedynką), więc jest liczbą pierwszą. Bierzemy ją w kółko, a jej wielokrotności wykreślamy. Znowu część jest już wykreślona, ale nie wszystkie warto się temu przyjrzeć bliżej. 2×5 było już wykreślone jako wielokrotność liczby 2. Liczba 3×5 to wielokrotność 3, też była wykreślona. Kolejna wielokrotność to 4×5, które jest wielokrotnością 4, czyli również 2. Następna wielokrotność, 5×5=25, to pierwsza “nowa” wielokrotność, którą wykreślamy na tym etapie.
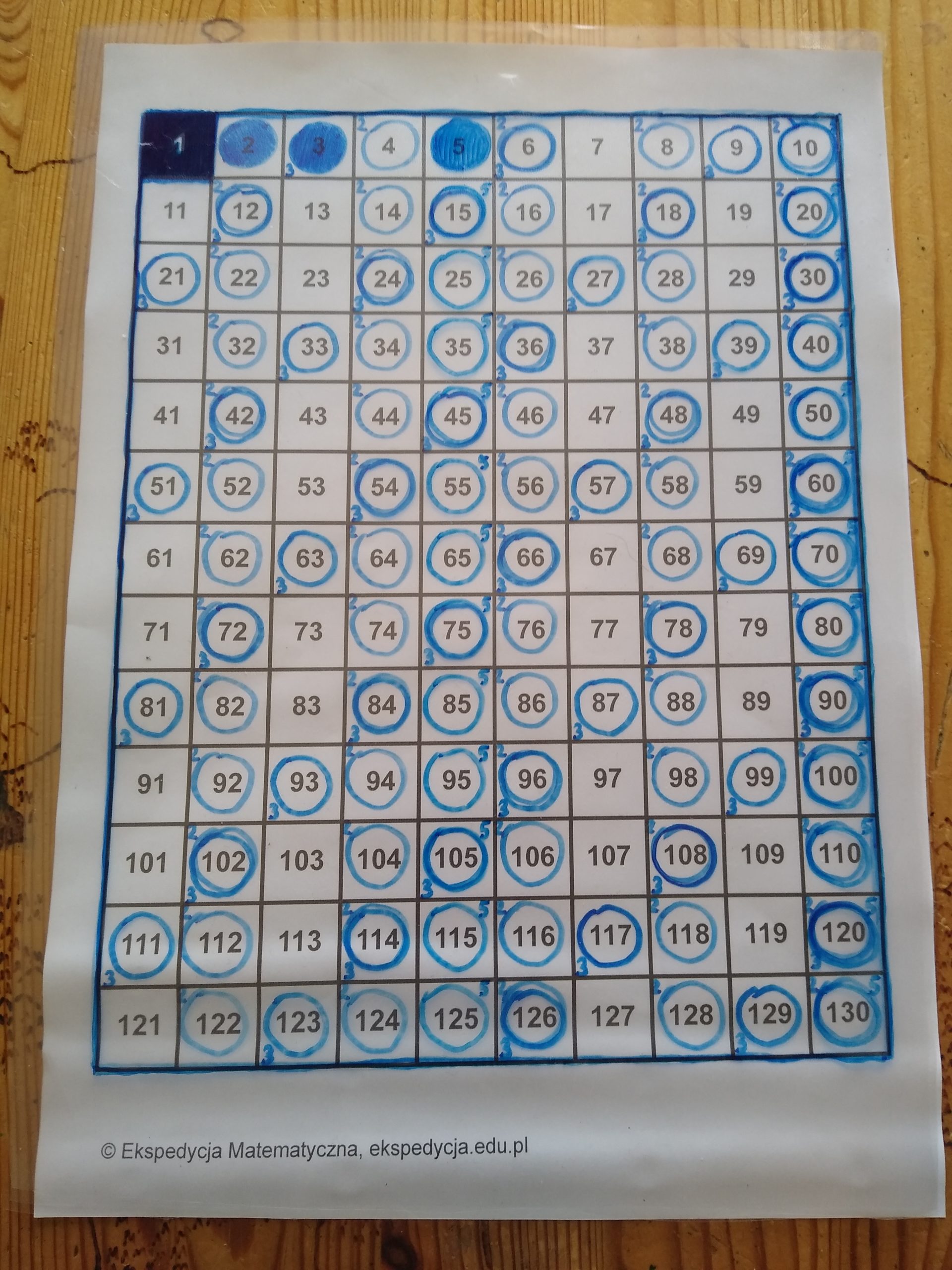
Następną liczbą jest 6. Sytuacja jest tu podobna jak z liczbą 4 – ponieważ jest to liczba złożona (poznajemy to po tym, że była już wcześniej wykreślona), to wszystkie jej wielokrotności są już wykreślone, bo są wielokrotnościami liczb 2 i 3. Jeśli dziecko nie jest o tym przekonane, pozwólmy mu to sprawdzić!
Teraz kolejna liczba pierwsza, czyli 7. Zaznaczamy ją, a następnie musimy zadbać o wykreślenie jej wielokrotności – choć 2×7, 3×7, 4×7, 5×7 i 6×7 zostały już wcześniej wykreślone, ale 7×7=49 to “nowa” liczba złożona, którą wykreślamy.
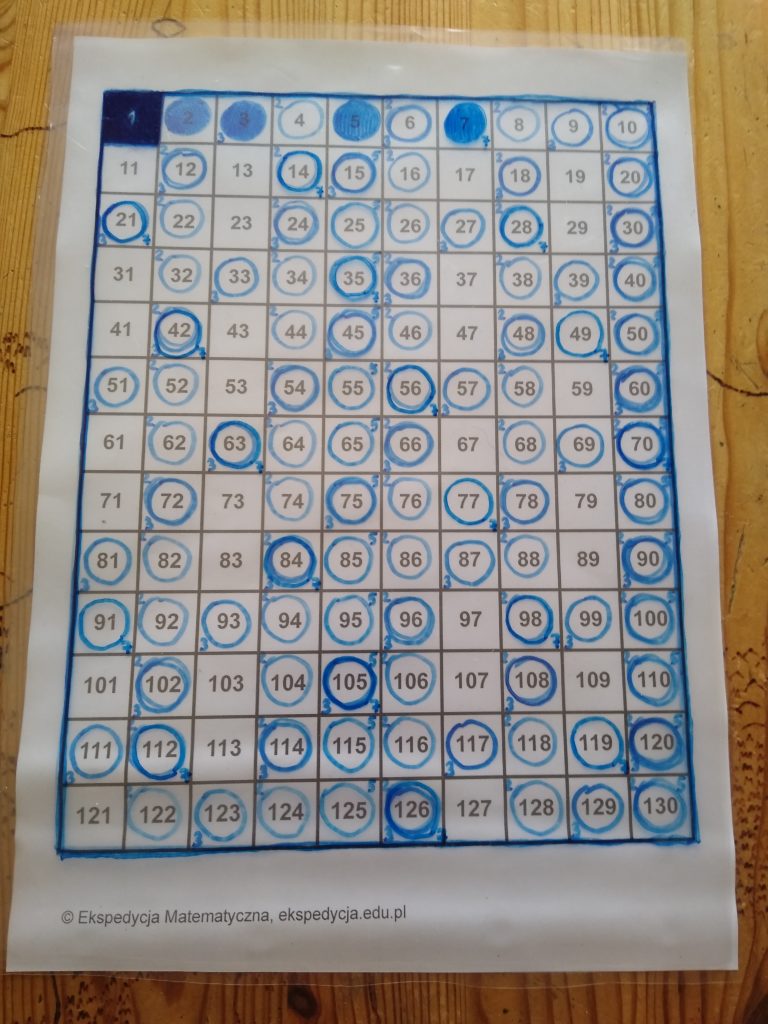
Liczby 8, 9 i 10 są złożone, więc podobnie jak przy liczbach 4 i 6, ich wielokrotnościami nie musimy się zajmować. Musimy za to zająć się liczbą 11, ponieważ nie została wykreślona przy wcześniejszych liczbach, więc jest liczbą pierwszą. Zaznaczamy ją sobie i wykreślamy jej wielokrotności: 2×11, 3×11 aż do 10×11 są już co prawda wykreślone, ale musimy wykreślić 11×11=121.
Kolejną liczbą pierwszą, którą musimy rozważyć jest 13. Ale okazuje się, że jej wielokrotności są już wykreślone, aż do… 13×13=169, które nie mieści się już w naszej tabeli. Gdyby tabela była większa, musielibyśmy wykreślać wielokrotności 13 i kolejnych liczb pierwszych, ale w tej nie musimy – nic nowego byśmy nie wykreślili. To oznacza, że wszystkie pozostałe nieokreślone liczby są liczbami pierwszymi.

W ten sposób znaleźliśmy wszystkie nasze “cegiełki” aż do 130. Jest ich całkiem sporo, ale też są rozłożone nieregularnie. Warto opowiedzieć dzieciom o tym, że szukanie bardzo dużych liczb pierwszych jest ważnym zadaniem (choć robi się je na komputerze w inny sposób) i przydaje się między innymi w używanych w dzisiejszych czasach szyfrach.
A już wkrótce zabierzemy się za budowanie z naszych cegiełek 🙂





