Proste? Trudne? Co osoba, to inne doświadczenia z liczbami rzymskimi. Rzeczywistość polskiej szkoły nie wspiera ich spokojnego wprowadzania – zwykle w rozkładzie materiału niewiele jest na nie czasu na matematyce. Według proponowanego rozkładu materiału “Matematyki z Plusem” wydawnictwa GWO poświęca się na nie 1 lub 2 lekcje w czwartej klasie. Natomiast “Matematyka z kluczem” zaplanowała na to tyle samo czasu, ale w klasie piątej (w czwartej pojawiają się liczby rzymskie do 40). A na historii bardzo szybko zaczynamy ich używać… wpierw do oznaczeń wieków, więc w ograniczonym zakresie, ale potem pojawiają się daty na zabytkach czy teksty źródłowe… Ze smutkiem obserwuję dzieci, które zniechęcają się i do matematyki, i do historii, tylko dlatego, że nie zdążyły opanować liczb rzymskich w narzuconym błyskawicznym tempie.
Jak wesprzeć dziecko w odkryciu i zrozumieniu liczb rzymskich? Takich działań z naszej strony może być co najmniej kilka. Przede wszystkim musimy sami zrozumieć, jak system rzymski działa i co w nim może być łatwe, a co trudne. Ważna jest też izolacja trudności, podzielenie nauki na etapy. Bardzo pomocne są też precyzyjne zasady tworzenia liczb w systemie rzymskim. Przeglądając podręczniki przekonałam się, że nie zawsze jest to oczywiste. Zasady są podane w zawiły sposób, w dziwnej kolejności, a do tego wymieszane z różnymi własnościami liczb rzymskich, które do ich zapisywania nie są potrzebne. W zachęceniu dzieci do poznawania systemu rzymskiego może być wielka opowieść o powstaniu liczb. Opowieść, która pozwoli rozbudzić zainteresowanie, by dziecko mogło poznawać je z wewnętrzną motywacją.
System rzymski – jak go używać i co może w nim być trudnego?
Pierwszym elementem, z którym się styka dziecko, są zupełnie inne znaki, których używamy do zapisu liczb. Dla większości dzieci zapamiętanie tych 7 symboli nie stanowi większego problemu, choć warto zastanowić się, co zrobić, aby zapamiętało to na trwałe. Tu kluczowa jest motywacja wewnętrzna dziecka i jego własna chęć do zgłębienia tematu. Dla dzieci z zacięciem historycznym lub graficznym pomocna może być informacja o tym, skąd właśnie takie oznaczenia na 1, 10, 50, 100, 500 i 1000. Można ją znaleźć np. na stronie histurion i doskonale wpleść w opowieść o powstaniu liczb.
Kolejną kluczową sprawą jest to, że podobnie jak w systemach pozycyjnych, kolejno zapisujemy liczbę tysięcy, setek, dziesiątek i jedności. Inaczej jednak niż w systemie dziesiętnym, np. ta sama liczba setek i dziesiątek jest oznaczona w inny sposób. To na tym etapie dziecko powinno zobaczyć, jak zapisać liczby 1, 2, 3, …, 9, oraz wszystkie “okrągłe” liczby: 10, 20, …, 90, 100, 200, …, 900, 1000, 2000 i 3000. Widać wtedy doskonale zależności w ich budowie – np. 4, 40, 400 mają tę samą budowę, ale skonstruowane są z innych znaków, odpowiadających. W zależności od dziecka, możemy pokusić się o opowieść, dlaczego właśnie tak – że gdy znak odpowiadający mniejszej liczbie poprzedza taki symbolizujący liczbę większą, to liczby odejmujemy. Taki sposób zapisu pozwala na zmniejszenie liczby użytych symboli, ale dzieciom potrafi przysporzyć nieco kłopotów.
Kolejny etap wydaje się prosty – zestawiamy obok siebie zapis poszczególnych pozycji, np. zapisując 2438 zestawiamy MM, CD, XXX i VIII obok siebie, otrzymując poprawny zapis liczby w systemie rzymskim. Jeśli poprzednie etapy są dobrze opanowane przez dziecko, to z zapisywaniem dowolnych liczb nie powinno już mieć problemów. Dzięki takiej kolejności nauki i podziałowi na etapy dziecko powinno uniknąć błędnych prób zapisu liczb takich jak 19 (czasem zapisywane błędnie jako IXX) lub 49 (które aż kusi do zapisania jako IL, ale powinno być zapisane jako XLIX). Na tym etapie, co nieraz zaskakuje dorosłych, dziecko niekoniecznie poradzi sobie z odczytywaniem tych liczb! To dlatego, że nie wiadomo, jak podzielić liczbę w systemie rzymskim na poszczególne pozycje dziesiętne. Faktycznie, może to nie być oczywiste, ponieważ ten sam symbol może występować w dwóch różnych pozycjach (np. C występuje w setkach lub w wyjątkowej sytuacji w dziesiątkach, jako część XC). Warto być świadomym, że może to być problemem, i izolować trudności w poznawaniu liczb rzymskich. Tylko jak to zrobić w praktyce…?
Wśród pomocy montessoriańskich można znaleźć pomoc z rzymską tablicą setki. Jest to tablica 10×10 zawierająca na polach liczby od 1 do 100, natomiast na żetonach (tego samego rozmiaru co pola) również liczby od 1 do 100, ale zapisane w systemie rzymskim. Jeśli młodsze dzieci są nią zainteresowane, to może stanowić to doskonałe wprowadzenie do poznawania systemu dziesiętnego. Mogą tam zaobserwować pewne zależności, poznać pierwsze symbole liczb rzymskich. Z doświadczenia wiem jednak, że to za mało. Dlatego proponuję własne rozwiązania, spójne z metodą Montessori – mam nadzieję, że będą przydatne!
Moja propozycja wprowadzania liczb rzymskich
Znając dziecko musimy odpowiedzieć sobie na pytanie, jak dużo jest w stanie poznać naraz. Jeśli liczby rzymskie w zakresie do 3999 (tak jak w podstawie programowej) będą za dużym wyzwaniem, możemy rozpocząć od mniejszego zakresu (np. do 399, by używać 5 symboli). Za każdym razem kolejność etapów będzie jednakowa, wystarczy odpowiednio ograniczyć proponowane materiały. Po jakimś czasie można poszerzyć poznany zakres, znów przechodząc przez wszystkie etapy.
Może wydawać się, że to nadmiar pracy przy tak prostym zagadnieniu. Zapewniam, że pracy nie jest więcej. Jest ona po prostu uporządkowana, zwykle każdy etap można “przejść” szybko. Jeśli tak będzie – krok po kroku dojdziemy do celu. Jeśli nie – będziemy dokładnie wiedzieli, z czym dziecko ma problem i damy mu czas, by go pokonało.
Etap I – wprowadzenie symboli
Ten etap można doskonale połączyć z opowieścią o historii liczb. Jeśli dziecko ma problem z zapamiętaniem większej liczby symboli, możemy pomyśleć o jej zmniejszeniu lub przeróżnych ćwiczeniach wspierających zapamiętywanie (memory, przeróżne zagadki, gry, wierszyki – to już najlepiej oceni rodzic/nauczyciel, znający dziecko). Najważniejsze jest to, że dziecko nie musi znać na pamięć wszystkich symboli przed wejściem w kolejny etap – to kolejne etapy są najlepszym sposobem do nieustannego powtarzania i używania, a przez to głowa “sama” je zapamięta. Jeśli więc dziecko nie zapamiętuje szybko, potrzebuje na to więcej czasu, umieśćcie przed sobą wypisane wszystkie symbole, z których będziecie korzystać.
Etap II – wprowadzenie “okrągłych” liczb

Na tym etapie prezentujemy dziecku zapis kolejnych “okrągłych” liczb. Aby mieć je przed oczami, warto wybrać te odpowiednie z tabliczek do złotego materiału (odkładamy liczby większe niż 3000). Ja lubię robić to, układając poszczególne liczby z żetonów z symbolami. Zaczynam od symboli dotyczących jedności, mówiąc: “Mam tu żetony z symbolem I, z symbolem V i jeden żeton z napisem IX. To dlatego, że X może pojawić się w zapisie jedności tylko w jednej wyjątkowej sytuacji, gdy jest poprzedzony znakiem I”. Następnie wyjaśniam, że jeśli obok siebie stoją jednakowe znaki, to je dodaję, podobnie jest gdy znak oznaczający większą liczbę stoi pierwszy. Jeśli znaki stoją w odwrotnej kolejności, to wówczas odpowiednio je odejmujemy. Odejmowanie będzie nam potrzebne, by krócej zapisywać liczby.
Po takim wstępie obok każdej możliwej liczby jedności (od 1 do 9) umieszczamy odpowiedni zapis, odpowiednio go komentując:
- liczbie jeden odpowiada symbol I (i kładziemy odpowiedni żeton)
- dwie jedności możemy oznaczyć dwoma takimi żetonami (kładziemy dwa żetony z I jeden przy drugim)
- trzy jedności oznaczamy trzema żetonami (kładziemy trzy żetony z III)
- cztery to pięć odjąć jeden, dlatego możemy ułożyć je z żetonów I i V. Żeton V musi być drugi, bo taka kolejność oznacza odejmowanie.
- pięć to symbol V
- sześć to pięć dodać jeden, dlatego możemy ułożyć je z żetonów V i I. Tym razem większą liczbę stawiamy najpierw, ponieważ dodajemy.
- siedem to pięć i jeszcze dwa (kładziemy żetony VII)
- osiem to pięć i jeszcze trzy (kładziemy VIII)
- dziewięć to dziesięć odjąć jeden. To ta wyjątkowa sytuacja, kiedy do zapisania jedności użyjemy symbolu oznaczającego dziesiątkę. Musimy poprzedzić go symbolem I, ponieważ odejmujemy 1.

Podobnie układamy liczby 10, 20, …, 90, następnie 100, 200, …, 900, a na końcu 1000, 2000 i 3000. Możemy wyjaśnić, że nie ma ogólnie przyjętego znaku na 5000, dlatego nie zajmujemy się większymi liczbami.
Jeśli dziecko szybko dostrzeże zasadę, może spróbować włączyć się w układanie. Jeśli nie – po zakończeniu zbieramy żetony i prosimy by teraz dziecko spróbowało. Warto przygotować wcześniej odpowiednią liczbę żetonów – staje się ona kontrolą błędu w tej pomocy (jeśli jakąś liczbę źle zapiszemy, zabraknie nam żetonów do innej lub pozostanie nadmiarowy żeton).
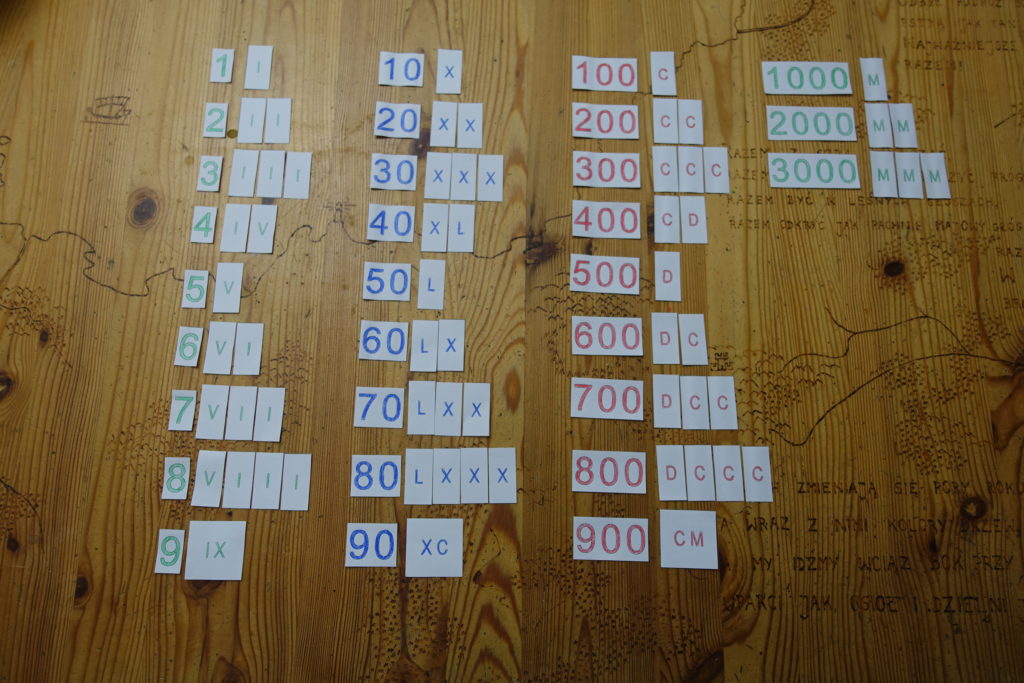
Do kolejnego etapu przechodzimy, gdy dziecko rozumie zasady zapisu wszystkich “okrągłych” liczb z zakresu, nad którym pracujemy. Nie musi jeszcze zapisywać ich w sposób mechaniczny, automatyczny, ważne po prostu, by umiało to zrobić. Ćwiczyć tą umiejętność będzie na kolejnym etapie.
Niezależnie od tego, czy zaprezentujecie to w taki sposób jak ja, czy inny, pomocna może być Baza 6. Jeśli ją wypełnicie, może być doskonałym miejscem, do którego dziecko może wracać, jeśli będzie miało potrzebę, na kolejnych etapach.
-
 Baza 60,00 zł
Baza 60,00 zł -
 Żetony liczb rzymskich0,00 zł
Żetony liczb rzymskich0,00 zł
Etap III – zapisywanie liczb arabskich w systemie rzymskim
Jeśli dziecko przeszło poprzedni etap, teraz nie powinno mieć większych problemów – wystarczy bowiem, że zestawi obok siebie zapis poszczególnych części liczby. Na przykład zapisując liczbę 2389, zapisuje 2000 (MM), 300 (CCC), 80 (LXXX) i 9 (IX), a następnie zestawia je obok siebie: MMCCCLXXXIX.
Przykłady do rozwiązywania na tym etapie możecie znaleźć w Bazie 7.
-
 Baza 70,00 zł
Baza 70,00 zł -
 Pomoc do zamiany liczb rzymskich i arabskich0,00 zł
Pomoc do zamiany liczb rzymskich i arabskich0,00 zł
Ten podział liczby na poszczególne pozycje dziesiętne doskonale wykonuje się na tabliczkach do złotego materiału. Jeśli jeszcze nie przychodzi to dziecku naturalnie, warto pracować właśnie z tabliczkami.
Niektórym dzieciom podoba się również zaproponowana przeze mnie pomoc, w której można “ustawiać” liczbę w systemie rzymskim, przesuwając odpowiednie paski. Jej wykonanie opisuję w dalszej części.
Etap IV – odczytywanie liczb rzymskich
Na początku możemy zaproponować dziecku odczytywanie liczb rzymskich, w których poszczególne pozycje dziesiętne są wyróżnione kolorami. Takie przykłady znajdziecie w Bazie 8. Jeśli doszliście z dzieckiem do tego etapu, to nie powinno mieć większych problemów z rozwiązaniem przykładów. Kolejnym, ostatnim już krokiem, jest dla dziecka samodzielny podział liczb i ich odczytywanie. Takie przykłady można znaleźć w Bazie 9.
Na tym etapie warto odwołać się do tego, co dziecko mogło już zaobserwować: że każdy znak ma swoją ustaloną pozycję dziesiętną, na której występuje. Wyjątki od tej reguły zdarzają się tylko wówczas, gdy jest poprzedzony znakiem z mniejszej pozycji dziesiętnej (np. C poprzedzone znakiem X należy razem z tym X do pozycji dziesiątek, a nie setek). To właśnie te wyjątki sprawiają, że pojawiają się problemy z odczytywaniem liczb, jednak dzięki wcześniejszym etapom, takie sytuacje powinny być przez dziecko stosunkowo łatwo identyfikowane.
Możemy również pozwolić dziecku na samodzielne odkrycie tego, jak dokonywać takiego podziału – ponownie możemy wykorzystać pomoc z przesuwanymi paskami. Chcąc odczytać jakąś liczbę musimy ustawić ją “w okienkach” – da się to zrobić tylko na jeden sposób, właśnie ten odpowiadający prawidłowemu podziałowi.
Skąd wziąć materiały?
Opisane pomoce można stosunkowo łatwo wykonać samodzielnie. Jeśli chciałbyś je wydrukować, zapraszam do poniższych linków.
Żetony do nauki zapisu “okrągłych” liczb możesz wykonać samodzielnie, zapisując odpowiednie symbole odpowiednim kolorem lub na odpowiednim tle. Potrzebować będziesz po 13 żetonów z symbolami I, X, C, po 5 żetonów z symbolami V, L, D, symbol M w 6 kopiach oraz 3 specjalne żetony (najlepiej podwójnych rozmiarów) z zapisami IX, XC oraz CM. Możesz zapisać je na kartonikach kolorowymi pisakami (lub białym/czarnym pisakiem na kolorowych kartonikach): te odpowiadające jednościom i tysiącom – na zielono, odpowiadające dziesiątkom – na granatowo, odpowiadające setkom – na czerwono.
Możesz też wydrukować gotowe żetony, w wersji kolorowej lub czarno-białej, w której możesz pokolorować cyfry. Jeśli nie masz tabliczek to układania zapisu liczb, również warto je przygotować (jeśli zamierzasz wykorzystać je tylko do pracy z liczbami rzymskimi, tabliczki z liczbami większymi niż 3000 możesz pominąć).
Pomoc z przesuwanymi paskami, przydatna do zapisywania i odczytywania liczb, jest równie prosta w wykonaniu. Możesz pobrać ją w wersji czarno-białej lub kolorowej.
-
 Pomoc do zamiany liczb rzymskich i arabskich0,00 zł
Pomoc do zamiany liczb rzymskich i arabskich0,00 zł -
 Żetony liczb rzymskich0,00 zł
Żetony liczb rzymskich0,00 zł -
 Tabliczki do złotego materiału0,00 zł
Tabliczki do złotego materiału0,00 zł

Wszystkie elementy wykonaj na sztywnym papierze lub zalaminuj. Jeśli nie masz laminarki, wzmocnij dodatkowo część z “okienkami” w miejscach, w których będą nacięcia (sporo daje nawet przyklejenie taśmy klejącej wzdłuż dłuższych krawędzi). Następnie wsuń w okienka kolejne paski, odpowiadające tysiącom, setkom, dziesiątkom i jednościom. I już!
Jeśli chcesz, możesz z drugiej strony pasków napisać cyfry arabskie, przy czym należy to zrobić uważnie, w odwrotnej kolejności (cyfra 1 musi być dokładnie w tym miejscu, co I, X, C i M), obrócone w taką stronę, by poszczególne cyfry ułożonej liczby były w dobrej kolejności (jedności po prawej, tysiące po lewej). Jeśli masz możliwość dwustronnego druku, możesz pobrać pomoc w wersji dwustronnej (uwaga! drukując ustaw “obróć stronę wzdłuż dłuższej krawędzi”). Oczywiście jeśli możesz drukować tylko jednostronnie, to możesz wyciąć paski umieszczone na obu kartkach, a następnie odpowiednio je skleić. Cyfry arabskie umieszczone po drugiej stronie mogą być wówczas jeszcze mocniejszą kontrolą błędu dla dzieci, które jej potrzebują (podstawową jest budowa materiału i układanie poprawnych liczb rzymskich oraz kolejność ułożenia symboli na paskach).
I co dalej…?
Warto korzystać z okazji do odczytywania i zapisywania liczb rzymskich. Najwięcej będą ich mieć pasjonaci historii, ale nie tylko! Pojawiają się w grach (np. jako oznaczenia kolejnych leveli – można pokusić się o taką numerację w samodzielnie tworzonej grze), oznaczeniach miesięcy, czasem jako numeracja rozdziałów książki… Warto szukać i przypominać sobie co jakiś czas to, co zostało już wypracowane. W ten sposób wiedza się utrwali i pozostanie w głowie na długo 🙂
Dajcie znać, jeśli potrzebne jest więcej inspiracji lub wskazówek do pracy! Mam ogromną nadzieję, że to co zgromadziłam w tym wpisie przyda się wam w pracy z dziećmi 🙂















5 komentarzy “Liczby rzymskie”
Super pomoc
Bardzo dziękuję! 🙂 Proszę dać znać, jak sprawdzi się “w akcji” z dziećmi 🙂
Znalazłyśmy dwa błędy w bazie 8 i 9
A tak poza tym to bardzo dziękuję 💚💛💜
Dziękuję, już poprawiałam 🙂 Własne błędy czasem trudno zauważyć, więc tym bardziej jestem wdzięczna za każdą zauważoną pomyłkę. W zakładce z bazami można już znaleźć poprawione wersje 🙂