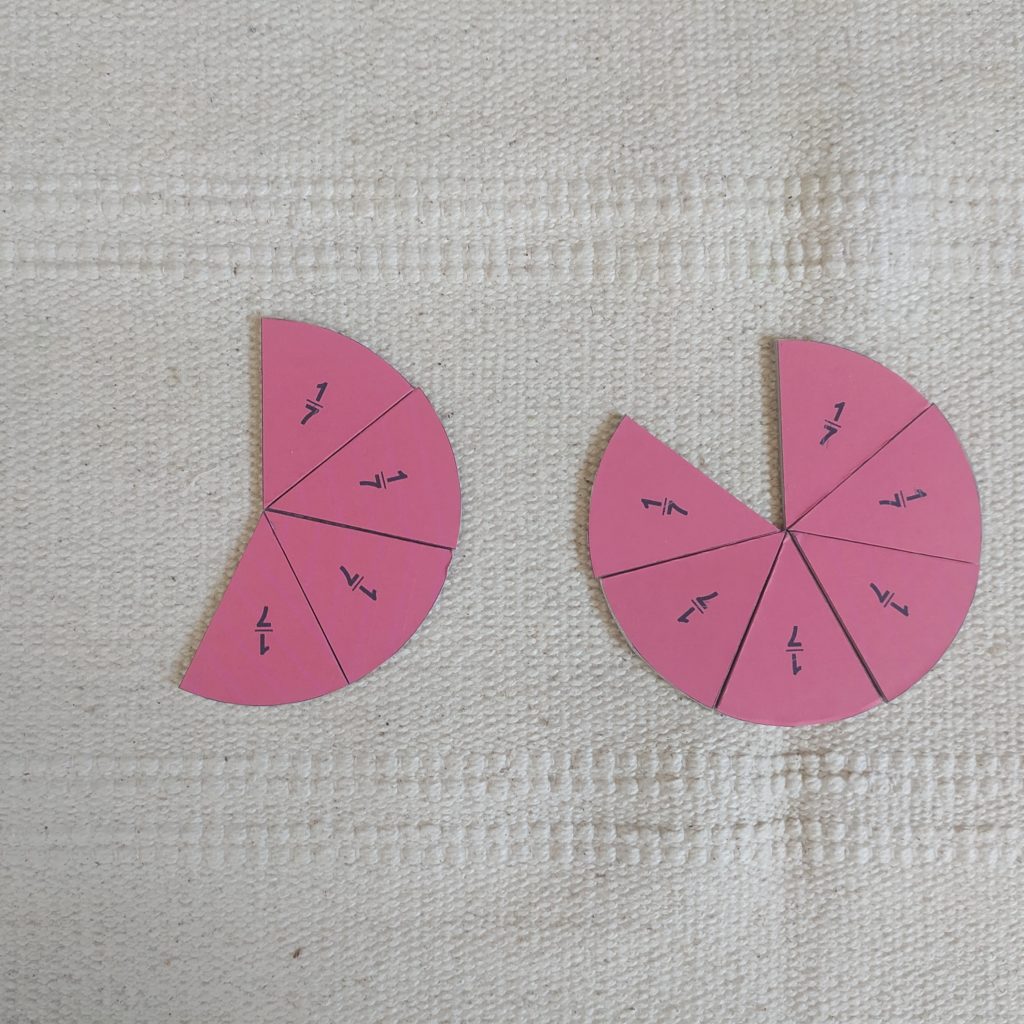Gdy nauczyciel matematyki myśli o dodawaniu ułamków zwykłych o tym samym mianowniku, zwykle czuje (sama tak miałam!), że to tylko pierwszy krok, że “prawdziwe” dodawanie ułamków zacznie się później, gdy trzeba będzie szukać wspólnego mianownika.
Jest w tym sporo prawdy – faktycznie dodawanie ułamków o różnych mianownikach jest zdecydowanie bardziej złożonym procesem, opierającym się o fundament dodawania przy jednakowych mianownikach. Tym bardziej jednak musimy zadbać o wszystkie elementy fundamentu, żeby móc budować dalej. Okazuje się, że trudności może pojawić się całkiem sporo już na tym etapie! Jednak jeśli wiemy o wszystkich, oddzielimy je, będziemy stopniować trudność, to jak zwykle droga krok po kroku okaże się osiągalna dla każdego 🙂
Jak zwykle będę pokazywać działania na montessoriańskiej pomocy. Osoby, które nie mają jeszcze montessoriańskich ułamków zwykłych, zapraszam do wpisu o tym, jak zrobić je samemu 🙂
Wszystkie opisane Bazy 75-78 (zestawy przykładów do rozwiązania, pogrupowanych według zdobywanej umiejętności) znajdują się poniżej:
Jak dodawać ułamki?
Dodawanie ułamków odbywa się na konkrecie dokładnie tak samo jak dodawanie liczb całkowitych. Tym razem jednak konkret jest trochę inny, a czasami musimy się trochę nagłowić, zanim wynik przedstawimy w takiej postaci, którą można zapisać.
Jeśli dodajemy dwa ułamki o tym samym mianowniku, nie powinno nam to nastręczyć większych kłopotów. Wystarczy ułożyć oba dodawane ułamki i zobaczyć, jaki ułamek tworzą razem?
O, proszę:
Już widać, że dwie siódme dodać cztery siódme to sześć siódmych.
A tutaj? Układamy trzy siódme i jedną siódmą i widać, że razem to…
cztery siódme!
Jeśli na tym etapie pracy na konkrecie pojawia się jakś kłopot, to źródło może być tylko jedno: trudności z układaniem i nazywaniem ułamków. Być może potrzebny będzie powrót do tego tematu 🙂
Co dodać, co przepisać…?
Pierwsze kłopoty, raczej drobne i chwilowe, mogą pojawić się na etapie przejścia do abstrakcji. Początkowo potrzebne jest spore skupienie, żeby z dwóch ułamków odczytać potrzebne do dodawania informacje i wykonać na nich odpowiednie operacje (mianownik przepisać, a liczniki dodać).
Jeśli dziecku sprawia to kłopot, dokładam etap przejściowy, na którym zadaje sobie kolejno pytania:
- jakie części dodajemy (tu trzeba sprawdzić mianowniki ułamków, na tym etapie powinny być jednakowe),
- jakie części otrzymamy (takie same – jeśli dodajemy części siódme, to otrzymamy części siódme, tutaj możemy już w wyniku wpisać mianownik,
- ile części dodajemy (tu wskazujemy na liczniki, np. dwie części siódme i cztery części siódme),
- ile części otrzymamy (dwie i cztery części to razem sześć, liczbę tę wpisujemy w liczniku wyniku).
Mając takie pytania, łatwiej jest przejść do abstrakcji. Takie podstawowe przykłady z dodawania ułamków zwykłych zebrałam w Bazie 75. Pierwsza część zawiera przykłady, które można wykonać na pomocy. Druga część wymaga już pracy abstrakcyjnej ze względu na większe mianowniki.
Przekraczanie całości
Zwykle pierwszym zaskoczeniem, które może nas spotkać, jest to, że suma dwóch ułamków może przekroczyć jeden. Spróbujmy dodać cztery siódme i sześć siódmych. Możemy zrobić to dokładnie tak, jak poprzednio. Tym razem po prostu wynik “nie mieści się” na jednym kole:
Co w takim razie? Można się zupełnie nie przejmować 😉 i liczyć tak jak poprzednio: otrzymamy części siódme i będzie ich 4+6=10. To oznacza, że wynikiem jest dziesięć siódmych. Możemy na tym poprzestać, ale też dobrze jest umieć zamienić taki wynik na liczbę mieszaną. Tutaj podkreślę, że nie zawsze, nie w każdym zadaniu i sytuacji warto to robić. Przyjęło się, by robić to co najmniej na końcu obliczeń. Oraz oczywiście wtedy, kiedy nam to umożliwi czy ułatwi obliczenia 🙂
Jak dokonać takiej zamiany? O tym pisałam już we wcześniejszym artykule. Teraz pora połączyć tę umiejętność z dodawaniem. Wykonujemy dodawanie, a potem “wyciągamy całości”. Zachęcam uczniów, by zapisali ułamek niewłaściwy otrzymany “po drodze” do ostatecznego wyniku.
Przykłady dodawania ułamków z przekraczaniem jedności zebrałam z Bazie 76. Podobnie jak w poprzedniej, pierwsza część bazy zawiera przykłady możliwe do wykonania na pomocy, a druga wprowadza w obliczenia abstrakcyjne.
Bardzo zachęcam też do poszukiwania strategii na sprytne wykonywanie obliczeń. Jedną z nich może być na tym etapie “dopełnianie” dużych części ułamkowych do całości. Opiszę to na przykładzie: będę dodawać pięć dziewiątych i osiem dziewiątych.
Standardowa metoda wygląda tak: wszystkich części dziewiątych jest ich 5+8=13. Od tego odejmujemy 9 części (one tworzą jedną całość), i uzyskujemy 13-9=4. Naszym wynikiem jest jeden i cztery dziewiąte.
Można pomyśleć inaczej: osiem dziewiątych to już prawie całość! Wystarczy przełożyć tam jedną dziewiątą z 5/9 i utworzyć całość. A poza całością? Mamy oczywiście 4/9, bo z pięciu dziewiątych zabrałam jedną część. Wynik oczywiście ten sam, czas też podobny, ale jak wiele może zmienić taka metoda przy dużych liczbach! Jeśli nie wierzycie, to spróbujcie dodać 386/451+449/451.
Obliczenia równoległe
Kolejnym wyzwaniem, z którym możemy się zmierzyć, jest dodawanie liczb mieszanych. Jak zwykle praca na konkrecie sprawia, że sam proces nie jest trudny do zrozumienia. Układamy obie liczby mieszane i patrzymy, jaką liczbę utworzą razem.
Powyżej liczby 1 i dwie siódme oraz 1 i trzy siódme. Dziecko w intuicyjny sposób łącząc liczby porządkuje elementy pomocy – oddzielnie całości (jest ich razem 1+1=2), a oddzielnie części siódme (jest ich razem 2+3=5). W takim razie w sumie otrzymujemy liczbę 2 i pięć siódmych.
Jakie wyzwanie może pojawić się przy przejściu do abstrakcji? Mamy tak naprawdę trzy procesy myślowe do wykonania jednocześnie. Dwa już znamy: mianownik pozostaje taki jak był (bo to rodzaj części, z jakimi mamy do czynienia), liczniki dodajemy (one mówią, ile części mamy). Dochodzi trzeci, polegający na tym, by obliczyć ile jest razem całości. Zwykle każdy z nich sam w sobie jest łatwy, ale niektórym dzieciom trudno skupić się na jednym, wykonać go i dopiero zająć się następnym. Taka umiejętność wymaga pewnej gotowości i ćwiczeń.
Jeszcze trudniej jest, gdy dochodzi kolejny etap – wyciąganie całości. Tutaj tym bardziej zachęcam dzieci do wykonania działania krok po kroku i zapisywania wyniku pośredniego.
Przykłady z dodawaniem liczb mieszanych zebrałam w Bazach 77 (bez przekraczania całości) i 78 (z przekraczaniem całości).
Czy wynik trzeba skracać?
Na początku przygody z dodawaniem nie zmuszam dzieci do skracania wyniku. Ze skracaniem wyniku jest podobnie jak z wyciąganiem całości – przyjęło się to robić, ale też czasem jest to zupełnie nieopłacalne, jeśli będziemy go używać w dalszych obliczeniach. Dlatego staram się pokazywać, dlaczego czasem warto skracać, a czasem nie.
Bazy 75-78 zawierają tylko przykłady, w których pojawiają się ułamki nieskracalne (żeby nawet nas-dorosłych nie kusiło do opowiadania o skracaniu, zanim nie ułożą się w głowie nowe umiejętności). Na skracanie wyników przyjdzie jeszcze czas. Jest to ważna umiejętność i dobrze ją ćwiczyć, ale… wszystko w swoim czasie 🙂