Jedynym z genialnych narzędzi do badania liczb naturalnych jest ich rozkład na czynniki pierwsze. W szkole nie mamy szans tego doświadczyć – co prawda używamy go do wyznaczania NWD i NWW liczb, ale bez zrozumienia, skąd wzięła się ta metoda, trudno więc docenić znaczenie samego rozkładu.
Zanim jednak zaczniemy korzystać z tego narzędzia, musimy je dobrze poznać. Żeby móc wykonywać rozkład liczby na czynniki pierwsze, dziecko potrzebuje kilku umiejętności:
- mnożenie i dzielenie (w zakresie liczb, które chcemy rozkładać – nie musi to być mnożenie czy dzielenie pisemne),
- umiejętność znajdowania dzielników liczby (o tym możesz przeczytać we wpisie o wielokrotnościach i dzielnikach),
- umiejętność rozpoznawania liczb pierwszych (początkowo można podpierać się tabelą liczb pierwszych, ale ważne by dziecko umiało sprawdzić czy liczba jest pierwsza – więcej o liczbach pierwszych można przeczytać we wpisie).
Jak zwykle ważna jest świadomość (nasza, jako rodziców czy nauczycieli) trudności, które musi pokonać dziecko, by w pełni opanować rozkład na czynniki pierwsze. Postaram się przedstawić tę naukę krok po kroku, zgodnie z zasadą izolacji trudności. W tym celu modyfikuję trochę metodę zapisu rozkładu na czynniki, znaną że szkoły. Nic nie stoi na przeszkodzie, by zapisywać to “tradycyjnie”, ale warto być świadomym wyzwań, z którymi mierzy się dziecko.
Do czego dążymy?
Naszym zadaniem jest przedstawienie zadanej liczby jako iloczynu liczb pierwszych. Liczby pierwsze są “cegiełkami” z których staramy się przez mnożenie uzyskać inne liczby. Czasem wystarczy tylko jedna cegiełka (jeśli liczba jest pierwsza, nie musimy już nic robić!), czasem potrzebne jest ich więcej. Jak będziemy znajdować te poprzednie? Dzieląc liczbę na coraz mniejsze kawałki, tak długo, aż wszystkie kawałki będą liczbami pierwszymi.
Krok pierwszy – dzielenie na kawałki
Proponuję, by początkowo nie oczekiwać od dziecka sprawdzania, czy liczba jest pierwsza, a jedynie poszukiwania dzielnika. Do tego etapu przygotowałam pomoc. Plik jest przygotowany na kolorowo, ale można bez problemu wydrukować go na czarno-biało (karty z liczbami pierwszymi będą wówczas szare zamiast zielone, ale nie ma to znaczenia, szczególnie że dodatkowo można je odróżnić rozmiarem). Jeśli ktoś woli wykonać wydruk na kolorowych kartkach, może skorzystać z pliku czarno-białego. Wtedy polecam wydrukować liczby pierwsze (te na kwadratowych kartach) na innym kolorze papieru niż pozostałe). Warto wydrukować również kartę kontrolną (w pomoc jest wbudowana tylko częściowa kontrola błędu w postaci rozmiaru kart).
Ważnym elementem jest teraz pokazanie dziecku, jak działa pomoc. Prezentując, zaznaczmy że liczby na zielonych latach to liczby pierwsze. Pozostałe to liczby złożone i będziemy starali się przedstawić je za pomocą mnożenia liczb pierwszych. Rozmiar karty jest zależny od liczby czynników pierwszych, które dana liczba ma w rozkładzie – tej informacji nie przekazujemy dziecku, ale jest ona pomocna rodzicowi/nauczycielowi w dobieraniu odpowiednich przykładów)
Trudność rozkładu danej liczby bardzo mocno zależy od umiejętności dziecka z zakresu pamięciowego opanowania tabliczki mnożenia (jeśli dziecko dobrze ją zna, to najprostsze do rozłożenia będą dla niego liczby z tabliczki mnożenia) i cech podzielności (jeśli je zna i sprawnie używa, to znacznie łatwiej będzie mu odkryć, że 2, 3, 5, 9 czy 10 są dzielnikiem danej liczby). Jednocześnie żadna z tych umiejętności nie jest konieczna – warto jednak być uważnym, czy żmudne obliczenia nie zniechęcają dziecka. Jeśli tak – lepiej poczekać na moment lepszego opanowania tabliczki mnożenia i cech podzielności.
Prezentację działania pomocy zacznijmy od takiej liczby, która ma dwa czynniki pierwsze (można to łatwo rozpoznać po rozmiarze karty, jest dwa razy większa od karty z liczbą pierwszą) dla której łatwo będzie dziecku wymyślić rozkład. Ja wybrałam liczbę 15. Znajdujemy odpowiednią kartę i kładziemy ją przed sobą. Teraz mówimy o tym, że 15 to 3 razy 5 i umieszczamy karty z liczbami 3 i 5 na karcie 15 (powinny całkowicie ją przykryć). To właśnie 3×5 jest rozkładem liczby 15 na czynniki pierwsze. Warto od razu ćwiczyć zapis i na kartce obok zapisać 15=3×5. Teraz kolej na dziecko: zaproponujmy mu karty podobnej trudności: 6, 10, 21. Podobnie może poradzić sobie z liczbami takimi jak 4, 9, 25 i 49 – tu pewnym zaskoczeniem może być to, że ten sam czynnik pierwszy może być użyty dwukrotnie.
Przedstawię teraz bardziej skomplikowany sposób użycia pomocy. Postaram się opisać go krok po kroku. Natomiast w dalszej części wpisu znajduje się informacja, jakimi etapami warto do tego dochodzić oraz co dalej?
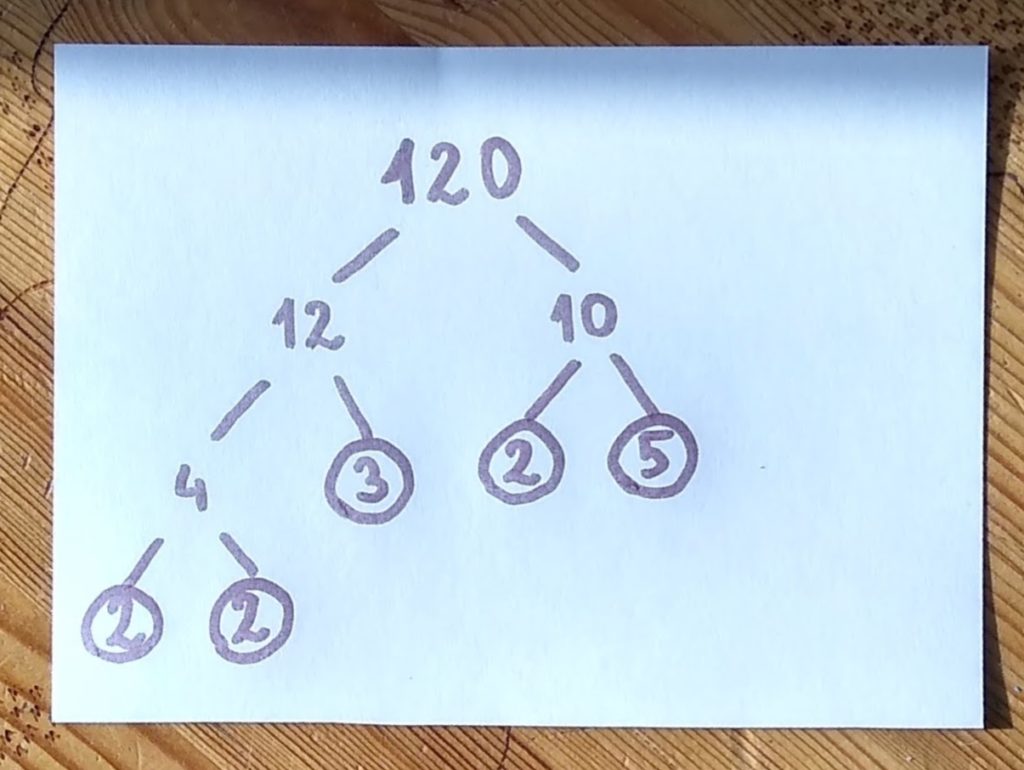
Popatrzmy, jak wygląda rozkład liczby 120 na czynniki pierwsze. Zaczynamy od położenia przed sobą liczby 120. Kolejne etapy pracy z pomocą można znaleźć na zdjęciach.





Oczywiście nie jest to jedyny sposób dojścia do takiego rozkładu – dziecko mogłoby zauważyć najpierw, że 120 to 2×60, a następnie rozkładać liczbę 60. Każda droga doprowadziłaby go do tego samego rozkładu (jest to dalece nieoczywiste! warto pozwolić dziecku spróbować, by sprawdziło różne sposoby), który różnił by się co najwyżej kolejnością czynników pierwszych.
Co dalej?
Na kolejnych etapach stopniowo utrudniamy. Jeśli dziecko ma opanowaną pamięciowo tabliczkę mnożenia, to proponuję taką kolejność kolejnych etapów:
- rozkładanie na czynniki pierwsze liczb pojawiających się w tabliczce mnożenia, początkowo złożonych z 2 lub 3 czynników pierwszych (są to prawie wszystkie liczby z tabliczki mnożenia, poza 16, 24, 32, 36, 40, 48, 54, 56, 60, 64, 72, 80, 81 i 90),
- rozkładanie liczb 16, 24, 32, 36, 40, 48, 54, 56, 60, 64, 72, 80, 81 i 90,
- rozkładanie liczb spoza tabliczki mnożenia.
Jeśli dziecko nie pamięta tabliczki mnożenia, ale zna cechy podzielności liczb, to możemy zaproponować mu następujące etapy pracy:
- liczby, które mają co najwyżej trzy czynniki pierwsze i co najwyżej jeden z nich jest inny niż 2, 3 lub 5 (takimi liczbami są wszystkie o 2 lub 3 czynnikach z wyjątkiem liczb 49, 77, 91, 98, 119),
- liczby z większą liczbą czynników pierwszych,
- liczby 49, 77, 91, 98 i 119 – dla tych liczb dziecko nie znajdzie żadnego dzielnika, korzystając ze “szkolnego” zestawu cech podzielności. Będzie musiało sprawdzić podzielność przez 7 (lub zauważyć podzielność przez inną liczbę).
Jeżeli natomiast dziecko nie zna cech podzielności, a tabliczkę mnożenia ma jeszcze słabo opanowaną, proponuję kierować się po prostu rozmiarem karty – zacząć od najkrótszych i stopniowo zwiększać długość. Przy każdym rozmiarze możemy postarać się wybrać liczbę, którą będzie dziecku łatwo rozłożyć (na przykład z zerem na końcu).
Krok ostatni – czy to już koniec?
Aby dziecko miało szansę przejść do etapu abstrakcyjnego znajdowania rozkładu na czynniki pierwsze, musi zdobyć jeszcze jedną umiejętność: rozpoznawania liczb pierwszych. Dzięki pomocy od razu widział, których fragmentów nie musi już dzielić na mniejsze. Jeśli nie ma do dyspozycji pomocy ani tabeli liczb pierwszych, nie będzie to oczywiste.
Tutaj bardzo przydają się doświadczenia z sita Eratostenesa! Musimy przypomnieć dziecku, że sprawdzenie czy liczba jest pierwsza, może ograniczyć się do sprawdzania podzielności przez kolejne liczby pierwsze. Jak długo? Dopóki wynik z dzielenia nie będzie mniejszy od liczby, przez którą dzielimy (zresztą – jeśli się zapędzimy, nic się nie stanie).
To dlatego nasz ostateczny algorytm rozkładu na czynniki pierwsze wygląda tak (fragment nawiązuje do karty z pomocy – dzielimy liczbę na fragmenty, aż każdy z nich okaże się liczbą pierwszą, cegiełką):
- jeśli jakiś fragment naszej liczby (a na początku po prostu całą liczbę) umiemy przedstawić w postaci dwóch liczb większych niż 1, to dzielimy go na dwa mniejsze fragmenty ,
- jeśli nie mamy pomysłu na to, jak zapisać jakiś fragment jako iloczyn, sprawdzamy jego podzielność przez kolejne liczby pierwsze (dzieląc lub korzystając z cechy podzielności): 2, 3, 5, itd.
- jeśli fragment jest podzielny przez jakąś z liczb pierwszych, wykonujemy dzielenie i zapisujemy fragment w postaci iloczynu dwóch mniejszych liczb,
- jeśli fragment nie jest podzielny przez żadną z liczb pierwszych (sprawdzaliśmy tak długo, aż wynik dzielenia przekroczył dzielnik), to znaczy, że jest to liczba pierwsza i fragment pozostaje jako cegiełka naszego rozkładu.
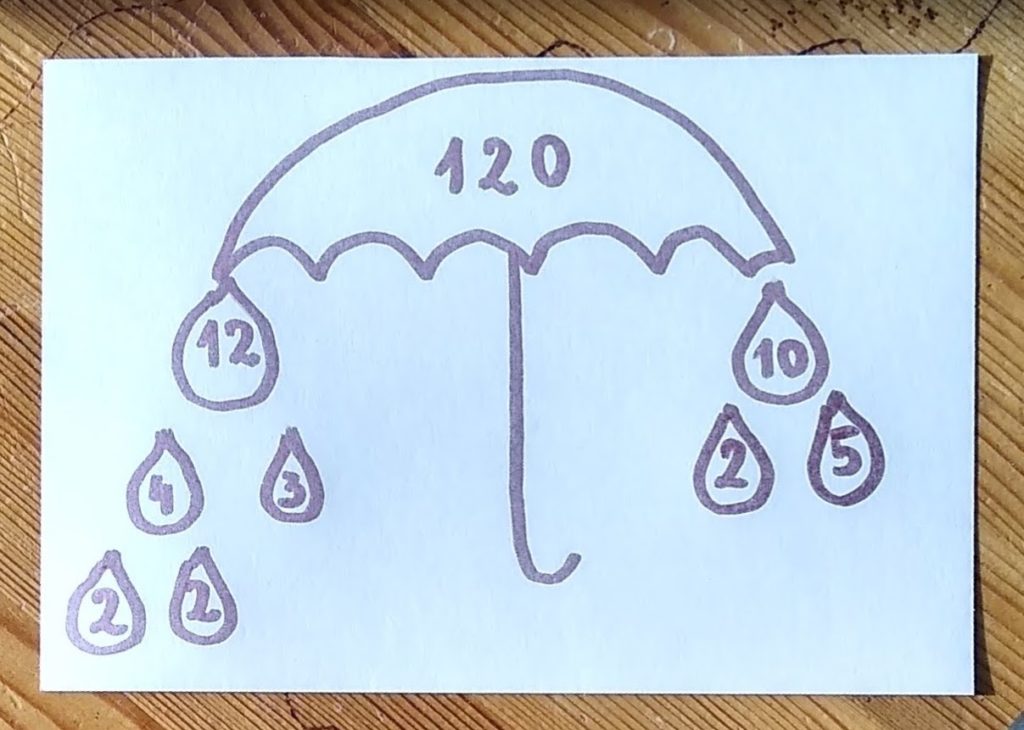
Zapis rozkładu na czynniki pierwsze w takiej formie wygląda inaczej niż w szkole (tam szukamy tylko dzielników pierwszych, nie pozwalamy zacząć od podziału 48=6×8). Można zapisywać go w formie “drzewka” jak na rysunku. Jeśli dziecko jest młodsze albo ma zamiłowanie artystyczne, może też spróbować formę graficzną – przykład znajduje się na zdjęciu. Dzięki temu można wpleść naukę rozkładu na czynniki pierwsze we wspaniałe tygodnie czy dni tematyczne!