Przygotowania do Ekspedycji, czyli o złotym materiale

Przygotowując Ekspedycję Matematyczną, skupiam się na realizacji podstawy programowej z matematyki dla klas 4-6. Jednocześnie wiele zagadnień jest dzięki pracy na konkrecie dostępna wcześniej. Warto więc spróbować wykorzystać Bazy do wspierania rozwoju młodszych dzieci, o ile tylko one same będą jakimś tematem zainteresowane.

Biorąc pod uwagę opracowywany zakres materiału, zakładam, że uczeń zna już wszystkie cyfry oraz rozumie istotę systemu dziesiętnego. Dziś chciałabym odpowiedzieć na potrzebę tych, którzy są jeszcze na etapie przygotowań do Ekspedycji i potrzebują zgłębić system dziesiętny.

Maria Montessori zaproponowała wspaniały materiał, który pozwala na dogłębne przeanalizowanie własności dziesiętnego zapisu liczby. Choć dla nas – dorosłych – jest on oczywisty, ponieważ używamy go nieustannie, to dla dzieci wcale taki nie jest. I trudno się dziwić! Wszak ludzie potrzebowali tysięcy lat, by wypracować taki właśnie zapis. Poniżej przedstawiam najważniejsze zasady budowy i działania złotego materiału, mam nadzieję, że praca z nim będzie doskonałym wstępem do Ekspedycji! W opisach staram się znaleźć złoty środek między jasnym i klarownym zapisem, a zebraniem wszystkich istotnych szczegółów. Jeśli nie masz doświadczenia pracy z materiałem montessoriańskim, zachęcam do zapoznania się najpierw z ogólnymi wskazówkami.

Tłumacząc swój pomysł na przygotowanie pomocy, Maria Montessori napisała w książce “Psychoarytmetyka” tak: “Jeśli przyjmiemy na przykład, że jedności oznaczają nauczycieli, dziesiątki – dyrektorów szkół, a setki – wizytatorów, to trudność występująca przy liczeniu dziewięciu wizytatorów nie jest większa niż przy liczeniu dziewięciu nauczycieli. Różnica między nimi polega wyłącznie na ich różnej funkcji społecznej, co nie wpływa na samą mechanikę liczenia od jednego do dziewięciu. Skoro tak to wygląda, przede wszystkim należy brać pod uwagę rzędy wielkości i zdawać sobie sprawę z ich wartości, aby nie potraktować omyłkowo wizytatora jak zwykłego nauczyciela […]. Zasadniczo wszystko sprowadza się do dwóch podstawowych faktów: przejścia z jednego rzędu do następnego – którego sekret tkwi w liczbie 10 – oraz dokładnego zrozumienia rzędów wielkości systemu dziesiętnego”. Budowa złotego materiału idealnie odpowiada tym wyzwaniom. Pozwala dzieciom uzmysłowić sobie najważniejszą własność systemu dziesiętnego – że ta sama cyfra ma różne znaczenie w zależności od pozycji, którą zajmuje w liczbie.

Budowa

Złoty materiał jest wykonany ze złotych koralików. Składa się z elementów reprezentujących poszczególne pozycje w systemie dziesiętnym. Są to:

• pojedyncze korale (umieszczone w miseczce) reprezentujące jedności,
• dziesięć korali połączonych w pręcik za pomocą drucika, odpowiadające dziesiątce,
• kwadrat złożony z dziesięciu połączonych pręcików, odpowiadający setce,
• sześcian złożony z dziesięciu kwadratów ułożonych jeden na drugim, reprezentujący tysiąc.

W zestawie do pracy w zależności od planowanych ćwiczeń, może być umieszczona różna ilość materiału. Zestaw minimum, pozwalający na podstawowe ćwiczenia (rozmienianie, łączenie, zapis liczb, dodawanie i odejmowanie) to 1 tysiąc, 18 setek, 18 dziesiątek i 100 jedności. Warto pokusić się o większy zestaw, np. 9 tysięcy, 45 setek, 45 dziesiątek i 100 jedności.

Do prezentacji materiału potrzebna jest również mata złożona z czterech coraz szerszych części (ich szerokość powinna być dobrana tak, by swobodnie układać materiał na odpowiednich częściach). Pierwsza (od prawej strony) jest ciemnozielona i służy do układania jedności. Druga, ciemnoniebieska, jest przeznaczona na dziesiątki. Trzecia, czerwona, pozwala na układanie setek. Czwarta ma ten sam ciemnozielony kolor, co pierwsza, i służy do umieszczania na niej tysięcy. Te kolory są niezwykle istotne, jeśli będziemy chcieli w przyszłości korzystać z innych pomocy Montessori – pozwalają zachować spójne oznaczenia kolorystyczne.

Potrzebne będą również tabliczki do układania zapisu liczb. Każda z tabliczek powinna być zapisana cyframi jednakowej wielkości, jednakowe powinny być również odstępy między cyframi. Dzięki temu, po odpowiednim nałożeniu tabliczek na siebie, tworzy się poprawny zapis liczby. Kolory cyfr na tabliczek są spójne z kolorami maty: tabliczki 1, 2, …, 9 mają ciemnozielone cyfry, tabliczki 10, 20, …, 90 – cyfry ciemnoniebieskie, tabliczki 100, 200, …, 900 – cyfry czerwone, natomiast tabliczka z 1000 (lub 1000, 2000, …, 9000, jeśli mamy więcej niż jeden tysiąc w złotym materiale) znów cyfry ciemnozielone.

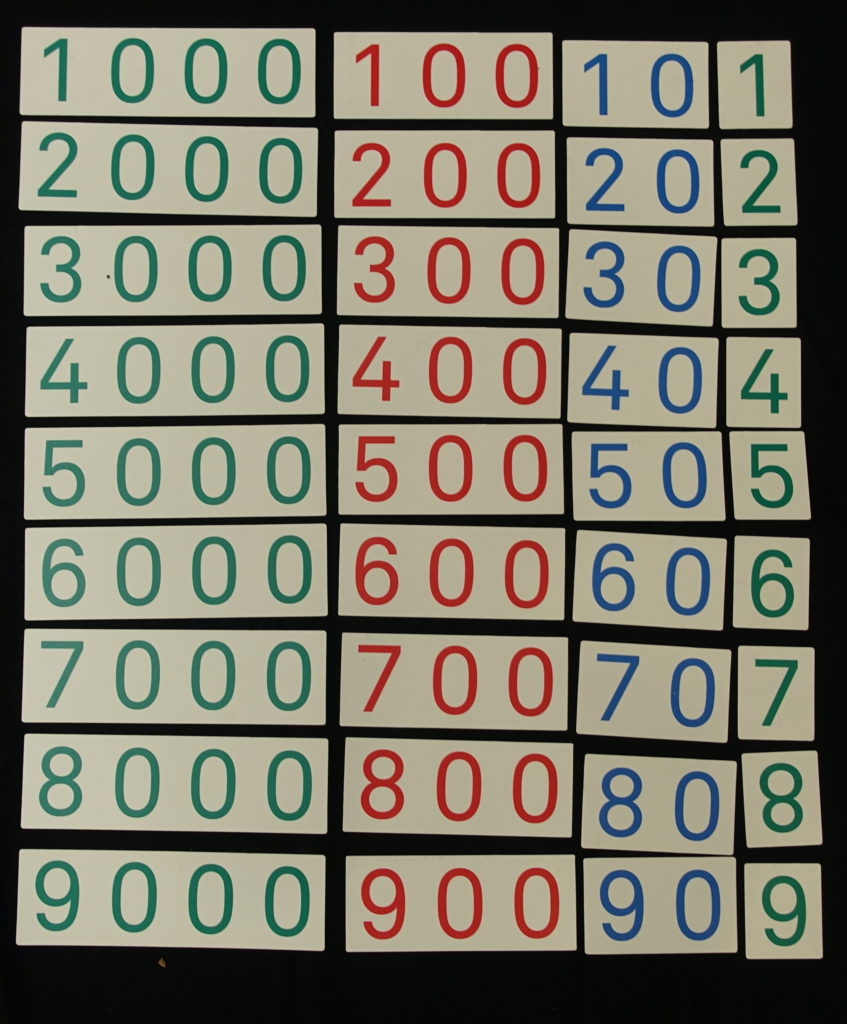
Jeśli chcesz – możesz pobrać tabliczki do druku:

Prezentacja i propozycje ćwiczeń na materiale

W czasie prezentacji należy przedstawić dziecku wszystkie elementy. Przy prezentacji złotego materiału warto podkreślić, że złota dziesiątka jest złożona z dziesięciu złotych jedności, złota setka – z dziesięciu złotych dziesiątek, a złoty tysiąc – z dziesięciu złotych setek.

Jeśli macie co najmniej 45 dziesiątek i setek, to pierwszym ćwiczeniem może być układanie liczb odpowiadających poszczególnym tabliczkom. Na dywaniku/stole układamy w kolejności tabliczki dotyczące jednej pozycji dziesiętnej (np. 10, 20, …, 90), a przy każdej z nich odpowiadającą jej liczbę ułożoną z materiału (tutaj będzie to jedna złota dziesiątka, dwie złote dziesiątki, …, dziewięć złotych dziesiątek). Jeśli nie mamy dostępnej tak dużej ilości złotego materiału, można układać wartość każdej tabliczki oddzielnie: Zaczynamy od jednej jedności i tabliczki z 1, następnie dokładamy kolejną jedność i kładziemy tabliczkę 2, itd. Podobnie postępujemy z dziesiątkami: kładziemy jedną złotą dziesiątkę i tabliczkę 10, dokładamy kolejną dziesiątkę i tabliczkę 20, itd.

Kolejnym (lub pierwszym) ćwiczeniem może być układanie dużych liczb. To ćwiczenie warto wykonywać już na macie. Należy przygotować złoty materiał, a tabliczki ułożyć obok maty. Zaczynamy od ułożenia pewnej liczby na macie ze złotego materiału (np. kładziemy na niej tysiąc, trzy setki, pięć dziesiątek i cztery jedności). Kolejny etap opisuję jako prezentację – jeśli pokażemy ją dziecku, w kolejnych powtórzeniach ćwiczenia, powinno dojść do samodzielnego wykonywania tych czynności. Zaczynając od jedności liczymy poszczególne elementy i wybieramy odpowiednią tabliczkę: w przykładzie liczymy jedności i kładziemy tabliczkę “4”, następnie liczymy złote dziesiątki i kładziemy tabliczkę “50”, liczymy setki i kładziemy “300”, a obok tysiąca kładziemy tabliczkę “1000”. Następnie nakładamy tabliczki na siebie (jedności na górze, a tysiące na dole) wyrównując je do prawej strony i tworząc zapis naszej liczby: 1354. Zaczynamy od liczb, które mają niezerowe cyfry, w dalszej pracy dodając również takie, w których pojawia się 0 (przy tym materiale nie jest to duża trudność – po prostu w jednym z rzędów nie wybieramy żadnej tabliczki, materiał jest tak przygotowany, że widoczne będzie wtedy w zapisie liczby zero z kolejnej tabliczki).

Analogicznym ćwiczeniem do poprzedniego jest układanie liczby na podstawie zapisu. Tym razem układamy liczbę za pomocą tabliczek i prosimy dziecko o ułożenie liczby ze złotego materiału.

Jeśli dziecko już dobrze zrozumiało zależność między liczbą ułożoną ze złotego materiału a jej zapisem, możemy przejść do przekraczania progów dziesiątkowych.

Możemy zrobić to na początku przy ćwiczeniu z układania dużych liczb. W pewnym momencie rozkładając liczbę, w jednej z pozycji dziesiętnych układamy więcej niż dziewięć elementów (np. 3 złote setki, 8 złotych dziesiątek i 10 złotych jedności). Dziecko próbując ułożyć zapis liczby powinno zauważyć, że nie ma odpowiedniej tabliczki (mamy dostępne tylko podpisy od 1 do 9). Możemy zapytać je, co w takim razie możemy zrobić, lub po prostu pokazać mu zamianę 10 jedności na złotą dziesiątkę. W ten sposób na macie pojawia się układ złożony z 3 złotych setek i 9 złotych dziesiątek, który można już bez problemu zapisać, używając tabliczek. Warto zacząć od takich ćwiczeń, w którym występuje jedno przekroczenie progu dziesiątkowego (najpierw z jedności do dziesiątek, później również w innych miejscach). To moment, w którym dziecko może samo zauważyć, dlaczego zapis najlepiej układać “od prawej do lewej”, czyli zaczynając od jedności. Dzięki temu zamiana w niższym rzędzie nie zmusza nas do wymiany tabliczki, którą wcześniej wybraliśmy (w przykładzie byłaby to zamiana tabliczki “80” na “90”). Jeśli dziecko samo tego nie dostrzeże, można mu to wyjaśnić i podkreślić, że jest to powód dla którego liczbę ułożoną ze złotego materiału zapisujemy “od prawej do lewej”. Następnie możemy pokazać takie przykłady, w których potrzebna będzie kilkukrotna zamiana (na jednej pozycji, jak np. 4 setki, 27 dziesiątek i 3 jedności lub na kilku pozycjach, jak np. 3 setki, 12 dziesiątek i 18 jedności). Warto szczególną uwagę zwrócić na przykład, w którym jedna zamiana wywołuje kolejną, np. 7 setek, 9 dziesiątek i 14 jedności. Dla dziecka układającego zapis liczby od prawej do lewej nie powinien on stanowić trudności, ale jeśli jakiś wcześniejszy etap nie został w pełni opanowany, to prawdopodobnie “wyjdzie” to tutaj.

Po tym ćwiczeniu dziecko jest gotowe do wykonywania na materiale dodawania dużych liczb. Podobnie jak w poprzednim ćwiczeniu, musimy zadbać o kwestię oddzielania poszczególnych trudności. Zaczynamy od przykładów, w których nie pojawia się przekraczanie progu. Układamy na tabliczkach dwie liczby, np. 215 i 473, a następnie prosimy dziecko o ułożenie ich ze złotego materiału. Warto układać te liczby, oddzielając je na macie niewielkim odstępem. Następnie pytamy o to, ile łącznie materiału leży na macie. Dziecko może odczytać i ułożyć wynik: 688. Warto robić to, porządkując materiał (zestawiając ze sobą te same pozycje dziesiętne z obu liczb) i zwracając uwagę na to, by odczytywanie działo się “od prawej do lewej” (jeśli dziecko nie ma jeszcze tego nawyku, warto wrócić do wcześniejszych ćwiczeń). Możemy również w tym momencie pokazać dziecku zapis dodawania pisemnego (zapisując składniki jeden pod drugim i prosząc dziecko o wpisanie wyniku, a w dalszej kolejności prosząc dziecko o zanotowanie całego działania).

Kolejnym krokiem w dodawaniu jest dodawanie dużych liczb z przekraczaniem progu dziesiątkowego. Przykłady warto zacząć od takich z jednym przekroczeniem progu, a wielokrotne przekraczanie pozostawić na dalszą pracę. Postępujemy podobnie jak poprzednio, zwracając szczególną uwagę na moment odczytywania wyniku (wymagający zamiany tam, gdzie pojawi się więcej niż 9 jednakowych elementów złotego materiału). Możemy też pokazać w tym momencie, w jaki sposób zaznaczyć taką zamianę w zapisie działania.

Na dalszym etapie nauki możemy zaproponować dziecku odejmowanie dużych liczb. Co ważne podkreślenia, w przykładach dotyczących odejmowania nie układamy z materiału obu liczb, a jedynie pierwszą z nich (odjemną). Następnie zabieramy liczbę odejmowaną (odjemnik) i dzięki temu możemy odczytać wynik. Warto od samego początku równolegle wprowadzać zapis pisemnego odejmowania. Nauka odejmowania przebiega w czterech etapach: bez przekraczania progu dziesiątkowego (gdy na każdej pozycji w odjemnej mamy tyle elementów, by móc zabrać ilość zgodną z odjemnikiem), z pojedynczym przekroczeniem progu dziesiątkowego, z kilkukrotnym przekroczeniem progu oraz z ostatnim, wymagającym bardziej złożonego “rozmieniania”. Ta ostatnia sytuacja ma miejsce na przykład w działaniu 1506 – 738, gdy chcemy przy zabieraniu ośmiu jedności rozmienić większy element. Ponieważ dziesiątki nie są dostępne, musimy najpierw rozmienić jedną ze złotych setek na 10 złotych dziesiątek, a dopiero potem jedną z nich rozmienić na jedności. Jest to dość złożona operacja, ale na złotym materiale przebiega w naturalny sposób.

Możemy również pokazać na złotym materiale mnożenie oraz dzielenie. Trzeba jednak zadbać o to, by w przykładach w żadnym momencie rozwiązywania nie zabrakło nam materiału, a to zwykle dość mocno ogranicza przykłady, które możemy dziecku zaproponować. Jeśli jednak czujemy, że dziecko jest gotowe i nie ma problemów z “zamianami” w systemie dziesiętnym, można już na tym etapie przejść na bardziej abstrakcyjną pomoc, jakim jest “gra w znaczki”. Jeśli jesteś nią zainteresowany, to zapraszam cię do wykonania własnych.

Ciekawym ćwiczeniem jest również analiza “łańcucha setki”. Można zakupić taki gotowy, ale możemy również przeprowadzić taką analizę z dzieckiem, korzystając bezpośrednio ze złotego materiału. Na początku prosimy dziecko, by rozmieniło złotą setkę na dziesiątki. Kiedy to zrobi, prosimy je o ułożenie otrzymanych w ten sposób dziesiątek w jednej linii (tak by początek kolejnej znajdował się tuż obok końca poprzedniej). Daje to doskonałe wyobrażenie o tym, jak duża jest liczba 100 w porównaniu z 1 i 10. Na uzyskanym w ten sposób łańcuchu możemy wykonywać rozmaite ćwiczenia: przeliczać korale od pierwszego aż do setnego, wskazywać konkretne korale (najpierw warto sprawdzić z dzieckiem, gdzie znajduje się dziesiąty, dwudziesty, trzydziesty itd. koral, a następnie szukać np. czterdziestego piątego). Strzałki do takiego łańcucha można pobrać w ramach pakietu do łańcuchów kwadratów liczb:

Możemy się pokusić również o analogiczną analizę “łańcucha tysiąca”. Do tego potrzebujemy jednak łańcucha złożonego ze stu dziesiątek. Jeśli macie dostęp do tylu (lub do gotowego łańcucha tysiąca), warto zacząć jego analizę od umieszczania zaznaczenia za pomocą strzałek wyróżnionych liczb. Za pomocą strzałek zielonych oznaczamy liczby 1, 2, 3, …, 9. Strzałkami niebieskimi zaznaczamy 10, 20, …, 90. Strzałkami czerwonymi zaznaczamy 100, 200, …, 900. Na samym końcu łańcucha kładziemy zieloną strzałkę 1000. Jeżeli takiego łańcucha nie macie, to warto porozmawiać z dzieckiem, jak myśli, jak długi byłby taki łańcuch? Z ilu dziesiątek by się składał? Gdybyście rozłożyli go na podłodze, to odkąd dokąd by sięgał? Jak można to odmierzyć (dziecko może zaproponować odmierzanie dostępnymi dziesiątkami, ale można to zrobić za pomocą łańcucha setki i będzie to bardzo pouczające).

Złoty materiał jest doskonały również do nauki podziału czasu w historii na wieki. Możemy ułożyć na podłodze oś czasu ze złotych dziesiątek (układamy je w jednej linii, idealnym rozwiązaniem jest połączenie ich końców w długi łańcuch). Następnie składamy je po 10, tworząc kwadraty (takie jak złote setki). Wykonując tę czynność, mówimy “tutaj znajdują się korale od pierwszego do setnego”, “tutaj znajdują się korale od sto pierwszego do dwusetnego” itd, umieszczając nad każdym kwadratem podpis “1-100”, “101-200” itd. Następnie mówimy dziecku o tym, że tak właśnie zostały podzielone w historii lata naszej ery, a każde sto lat nazywamy wiekiem. Następnie możemy podpisać każdy wiek. W dalszej kolejności możemy ćwiczyć z dzieckiem: “W którym kwadracie znajduje się dwieście czterdziesty siódmy koralik? W którym wieku był rok dwieście czterdziesty siódmy?”.

Skąd wziąć złoty materiał?

Zdecydowanie najłatwiej (i najdrożej ;)) jest złoty materiał kupić. To spory wydatek, ale trudny do zastąpienia. Na rynku można znaleźć dwa różne drewniane zastępniki. Jeden z nich (mniej popularny) składa się z odpowiednio połączonych drewnianych sześcianików. Dzieciom odrobinę trudniej jest dostrzec na nim zależności pomiędzy poszczególnymi pozycjami w systemie dziesiętnym, ale jest to generalnie całkiem sensowne budżetowe rozwiązanie. Sama z takiego korzystam. Nie polecam natomiast drugiego rozwiązania, jakim są drewniane kwadraty setek i sześciany tysięcy z namalowanymi kropkami, nawiązującymi do oryginalnej budowy z korali. Te oznaczenia są dla dzieci zupełnie niejasne (chyba, że mają już za sobą dłuższą pracę z oryginalnym materiałem, ale wówczas równie dobrze mogą już działać na znaczkach) i potrafią wprowadzić w błąd (na sześcianie tysiąca widać 600 namalowanych kropek, zupełnie niewidoczne jest, czemu jest to tysiąc).

Można oczywiście spróbować również wykonać złoty materiał samodzielnie, ale nie da się ukryć, że jest to bardzo czasochłonne. Kolor złoty nie jest najważniejszy (ale powinien wyróżniać się na tle pozostałych kolorów, jako ten kluczowy dla naszego zapisu liczb). Warto pokusić się o to, żeby faktycznie był złoty, jeśli jest to możliwe. Bardzo ważne są natomiast kolory maty i cyfr na tabliczkach – będą się one przewijały również w zapisie przykładów do rozwiązania na pierwszym etapie pracy z pomocą. Jeśli chcemy więc korzystać z wydrukowanych zadań (choćby Baz Ekspedycji), to spójność oznaczeń jest niezwykle ważna.

Matę do prezentacji materiału można natomiast wykonać spokojnie samodzielnie (szczególnie jeśli ktoś potrafi szyć – taka z bawełny jest idealna i wolę ją niż część dostępnych w sklepach).

Podobnie można zrobić tabliczki – wypisując je ręcznie lub drukując. Dobrą opcją jest ich zalaminowanie lub naklejenie na grubszy karton, by zwiększyć ich trwałość.

Co dalej?

Na dalszym etapie następuje wprowadzenie kolejnych pozycji dziesiętnych (dziesięć tysięcy, sto tysięcy, milion, dziesięć milionów itd.) oraz przejście na bardziej abstrakcyjny materiał, jakim są montessoriańskie znaczki. Jeśli masz dostęp do oryginalnych pomocy, to równie serdecznie zapraszam do kolejnych wpisów, które w zgodzie z montessoriańskimi pomocami pozwalają poznawać matematykę krok po kroku 🙂