Twierdzenie Pitagorasa pojawia się w szkole dość późno. Przyczyna jest prozaiczna – “typowe” zadania z jego wykorzystaniem wymagają biegłego obliczania kwadratów i pierwiastków liczb. Maria Montessori podeszła do niego zupełnie inaczej – dziecko może na wczesnym etapie doświadczyć prawdziwości twierdzenia. Jak? Bazując na polach figur. O nich zresztą jest przecież to twierdzenie! A nasza tendencja do zapisywania wszystkiego za pomocą liczb w tej sytuacji może stać się utrudnieniem zamiast ułatwieniem.
Zapraszam więc, by razem z dziećmi doświadczyć twierdzenia Pitagorasa!
Na samym początku – by sensorycznie doświadczyć “że działa”.
Na kolejnym etapie – by zobaczyć “dlaczego działa”.
A dopiero po opanowaniu kwadratów i pierwiastków – by obliczać długość boku trójkąta prostokątnego na podstawie pozostałych dwóch boków.
Wykroje na portki
Przygotowałam trzy zestawy układanek – jedna z nich dotyczy trójkąta o bokach w proporcjach 3:4:5, jedna – trójkąta prostokątnego równoramiennego, a dwie – dowolnego trójkąta prostokątnego (w układankach są to trójkąty przystające do tego z pierwszej układanki, ale poczynione obserwacje będą ogólne). Pierwsze trzy są bazowane na tradycyjnych pomocach Montessori. Czwarta jest prezentacją mojego ulubionego dowodu twierdzenia Pitagorasa 🙂
Wszystkie układanki można pobrać z plików:
-
 Twierdzenie Pitagorasa – plansza IV0,00 zł
Twierdzenie Pitagorasa – plansza IV0,00 zł -
 Twierdzenie Pitagorasa – plansza III0,00 zł
Twierdzenie Pitagorasa – plansza III0,00 zł -
 Twierdzenie Pitagorasa – plansza II0,00 zł
Twierdzenie Pitagorasa – plansza II0,00 zł -
 Twierdzenie Pitagorasa – plansza I0,00 zł
Twierdzenie Pitagorasa – plansza I0,00 zł
Najlepiej jest wyciąć elementy z tektury introligatorskiej lub innego “grubego” materiału (karton, pianka), żeby elementy dobrze się układało. Warto zwrócić uwagę, że potrzebne są nie tylko wycięte według wzoru elementy, ale też białe “zewnętrze”, powstałe po wycięciu wszystkich zaznaczonych elementów (nie są za to potrzebne wszystkie białe elementy – najlepiej po wycięciu przeczytać opis i dopiero wtedy wyrzucić niepotrzebne części).
Pierwsza przymiarka
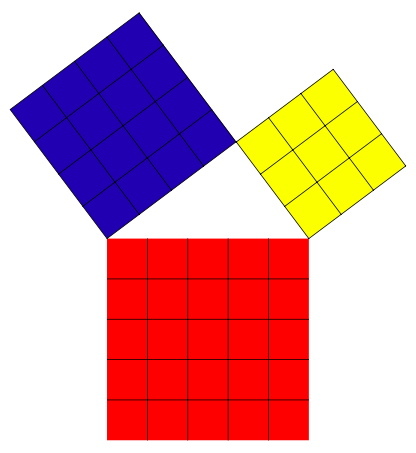
Pierwsza układanka pozwala doświadczyć twierdzenia Pitagorasa w szczególnym przypadku trójkąta o bokach długości 3, 4 i 5. Składa się z trójkąta prostokątnego oraz kwadratów na bokach, podzielonych na kwadraty jednostkowe. Każdy ma swój kolor – kwadraciki składające się na kwadrat o boku 3 są żółte, te w kwadracie o boku 4 są niebieskie, a tworzące kwadrat o boku 5 są czerwone.
Dziecko przekładając kwadraciki może sprawdzić, że dwa mniejsze kwadraty mają łącznie tyle kwadracików, co duży kwadrat. Może na przykład ułożyć małe kwadraty z czerwonych kwadracików, a duży kwadrat na przeciwprostokątnej – z kwadracików żółtych i niebieskich. U młodszych dzieci warto zostawić to na poziomie odkrycia: “tu i tu razem jest tyle co tu”. Nie trzeba więcej! Na kolejne komentarze możemy sobie pozwolić, gdy dziecko pozna trójkąty prostokątne (bo to właśnie dzięki temu, że kwadraty są zbudowane na bokach trójkąta prostokątnego, zachodzi odpowiednia równość) i pojęcie pola (już nie musimy mówić o liczbie kwadracików, możemy powiedzieć “pole”).
Ja nie ukrywam, że sama tej pomocy w domowych warunkach nie używam (ale w szkole – jak najbardziej!). To dlatego, że świetnie można wykorzystać w zastępstwie kolorowe liczby – takie jak moje zakupione, albo takie jak wydrukowane z działu Narzędzia. Do zapoczątkowania zabawy wystarczy wyciąć trójkąt prostokątny o długościach boków odpowiadającym kolorowym liczbom 3, 4 i 5 (będzie to 3cm, 4cm i 5cm w przypadku kupnych kolorowych liczb albo 6cm, 8cm i 10cm w przypadku tych wydrukowanych). Zaprośmy dziecko do zbudowania kwadratów na bokach trójkąta. A teraz zagadka – co ma większą wartość: dwa mniejsze kwadraty razem czy ten największy kwadrat? Możemy to świetnie sprawdzić obliczając (to starsi) lub układając obok siebie dwa łańcuchy. Najlepsze jest to, że możemy też eksperymentować z długością boków trójkąta – możemy pokusić się o boki 6, 8 i 10, a nawet 5, 12, 13 (tu już ciut trudniej ułożyć je z kolorowych liczb, ale można!). Możemy pójść jeszcze dalej – zobaczyć, co dzieje się w innych trójkątach o całkowitych bokach, i odkryć, że w trójkątach rozwartokątny ten największy kwadrat jest większy niż dwa mniejsze, a w ostrokątnych to dwa mniejsze kwadraty przeważają 🙂 Dowodu co prawda nie mamy, ale możemy zebrać naprawdę dużo danych doświadczalnych! 😉
W kolejnej pomocy możemy doświadczyć, że twierdzenie Pitagorasa jest również prawdziwe w trójkącie prostokątnym równoramiennym. Tam nie mamy możliwości pocięcia wszystkich trzech kwadratów zbudowanych na bokach na jednakowe kwadraciki (nie jest to wcale oczywiste, wynika z niewymierności pierwiastka z dwóch). Możemy mimo to poradzić sobie w inny sposób, dzieląc wszystkie kwadraty na trójkąty przystające do tego wyjściowego.
Pierwszym wyzwaniem jest zastąpienie kwadratów takimi trójkątami i jak widać na pierwszym zdjęciu – wcale nie jest to takie łatwe 😉 Kiedy już umiemy to zrobić, możemy zacząć eksperymenty – czy uda się zamienić miejscami czerwone trójkąty z tymi żółtymi i niebieskimi? Tak! I znów mamy kolejne doświadczenie w rękach, oczach i głowach 🙂 Ciekawe jest też to, że czerwony kwadrat jest dwa razy większy (w sensie pola) od kwadratu żółtego czy niebieskiego. A przecież jego bok nie jest dwa razy większy! 🙂 I znów – na proporcje pól figur podobnych przyjdzie jeszcze czas, ale już mamy do czego się odwoływać 🙂
Szczegółowe mierzenie
Kolejnym etapem będzie bardziej szczegółowe i ogólne przyglądanie się kwadratom na bokach trójkąta prostokątnego. U starszych może doprowadzić do pełnego dowodu twierdzenia Pitagorasa (a nawet do dwóch różnych dowodów). U młodszych może stać się mocną podbudową na przyszłość.
Pierwsza propozycja to trzecia z pomocy opracowanych przez Marię Montessori. Składa się z trzech plansz (oryginalnie jest jedna duża – możecie pokusić się o taki duży format). Zanim jednak omówię wszystkie (bardzo przydatne przy drugim sposobie pracy z pomocą), wykorzystamy tylko niektóre elementy. Przygotujmy elementy i planszę z pierwszej strony (to ta, która zawiera trójkąt prostokątny i zbudowane na bokach kwadraty) oraz dwa równoległoboki.
Zacznijmy od ułożenia “na miejscach” trójkąta i kwadratów. Teraz zabierzmy jeden kwadrat (proponuję na początku niebieski lub żółty), odłóżmy na bok i zachęćmy dziecko, by spróbowało tak przełożyć elementy, by ten kwadrat udało się zastąpić innym elementem. Okazuje się, że całkiem łatwo to zrobić – wystarczy przesunąć trójkąt i kwadratowy “otwór” zamienia się w taki o kształcie równoległoboku. Dzięki temu możemy przekonać się, że żółty kwadrat jest równoważny (w sensie równości pól) żółtemu równoległobokowi. Podobnie możemy odkryć, że niebieski kwadrat ma to samo pole co niebieski równoległobok. A jak jest z czerwonym kwadratem? Jeśli go zabierzemy i przesuniemy odpowiednio trójkąt, to z powstałej luce zmieszczą się oba równoległoboki. A w takim razie… czerwony kwadrat jest jak dwa równoległoboki, czyli też jak dwa kwadraty: żółty i niebieski!
Żeby powyższe doświadczenie stało się prawdziwym dowodem matematycznym, nie potrzebujemy wiele. Wystarczy zobaczyć, dlaczego “taki sam” żółty/niebieski równoległobok pasuje w oba miejsca. W tym celu możemy wyjąć wszystkie elementy i ułożyć np. niebieski równoległobok najpierw w jednym położeniu (gdy zastępował niebieski kwadrat), a potem w drugim (gdy zastępował część czerwonego kwadratu). Czym różnią się te położenia? Obrotem o kąt prosty (możemy to zaobserwować patrząc na boki, które pokrywają się bokami niebieskiego/czerwonego kwadratu w początkowym położeniu). Nic więc dziwnego, że to “ten sam” równoległobok 🙂
Zauważcie, że samo przekładanie i zamienianie figur może być również świetną zabawą sensoryczną. Układów zapełniających lukę jest dużo więcej. Dajmy dzieciom popróbować, pokombinować! Dzięki temu świetnie doświadczają przeróżnych geometrycznych zależności.
Z pomocą można też pracować inaczej, bardziej “tradycyjnie”. Będziemy również odkrywać figury o takich samych polach, ale wykorzystamy do tego dodatkowe plansze, znane już równoległoboki i dwa prostokąty (żółty i niebieski). Opierać się będziemy na znajomości wzoru na pole równoległoboku, dlatego taka praca z pomocą ma sens dopiero na konkretnym etapie. Dzięki planszom możemy odizolować porównanie pól konkretnych figur od innych zależności. Niektórym dzieciom ułatwia to pracę, inne wolą pierwszy sposób, w którym widzą “co to za figury”.
Poniżej wypisuję kolejne etapy prezentacji pracy z pomocą:
- zastępuję czerwony kwadrat dwoma prostokątami i komentuję: “czerwony kwadrat ma takie samo pole jak żółty i niebieski prostokąt”
- wyjmuję żółty kwadrat i biorę żółty równoległobok. Przymierzam odpowiednie boki (“równoległobok ma taką podstawę jak bok kwadratu”) i wkładam obie figury na drugiej planszy (“wysokość równoległoboku jest również taka, jak bok kwadratu). Komentuję teraz, że w takim razie żółty równoległobok ma to samo pole, co żółty kwadrat (mają odpowiednie podstawy i wysokości)
- wyjmuję niebieski kwadrat i biorę niebieski równoległobok. Przymierzam odpowiednie boki (“równoległobok ma taką podstawę jak bok kwadratu”) i wkładam obie figury na drugiej planszy (“wysokość równoległoboku jest również taka, jak bok kwadratu). Komentuję teraz, że w takim razie niebieski równoległobok ma to samo pole, co niebieski kwadrat (mają odpowiednie podstawy i wysokości)
- wyjmuję żółty prostokąt z pierwszej planszy i żółty równoległobok z drugiej. Przymierzam odpowiednie boki (“równoległobok ma taką podstawę jak długość prostokąta”) i wkładam obie figury na drugiej planszy (“wysokość równoległoboku jest taka, jak szerokość prostokąta). Komentuję, że w takim razie żółty równoległobok ma to samo pole, co żółty prostokąt (mają odpowiednie podstawy i wysokości)
- wyjmuję niebieski prostokąt z pierwszej planszy i niebieski równoległobok z drugiej. Przymierzam odpowiednie boki (“równoległobok ma taką podstawę jak długość prostokąta”) i wkładam obie figury na drugiej planszy (“wysokość równoległoboku jest taka, jak szerokość prostokąta). Komentuję, że w takim razie niebieski równoległobok ma to samo pole, co niebieski prostokąt (mają odpowiednie podstawy i wysokości)
- teraz wkładam kwadraty i prostokąty znów na pierwszą planszę. Pora na komentarz: żółty kwadrat ma takie samo pole jak żółty równoległobok, a ten ma takie samo pole jak żółty prostokąt. To oznacza, że pole żółtego prostokąta jest takie samo jak pole żółtego kwadratu. Tak samo możemy skomentować jednakowe pola niebieskiego prostokąta i kwadratu
- Skoro żółty prostokąt ma pole jak żółty kwadrat, niebieski prostokąt ma pole jak żółty kwadrat i razem tworzą czerwony kwadrat, to znaczy, że czerwony kwadrat ma takie pole jak żółty i niebieski kwadrat razem 🙂
Kolejna pomoc to moje autorskie przedstawienie znanego dowodu twierdzenia Pitagorasa (taką układankę opisywał między innymi S. Jeleński w “Lilavati”, a dowód był znany od starożytności). Lubię go, bo kryje w sobie też powiązanie w wzorem skróconego mnożenia. Do jego prezentacji potrzebujemy, poza kwadratami zbudowanymi na bokach trójkąta prostokątnego, czterech trójkątów prostokątnych (przystających do tego, na którym zbudowane są kwadraty) i odpowiednia kwadratowa luka 🙂
Jak zwykle możemy zaprosić dziecko do prób układania elementów na różne sposoby. Jak zapełnić kwadratową lukę za pomocą kolorowych kwadratów i trójkątów, które mamy? W ten sposób możemy zebrać ogrom doświadczeń i obserwacji 🙂
Jeśli chcemy zaprezentować dowód twierdzenia Pitagorasa używając tej pomocy, możemy zrobić to na przykład tak:
- wyjmujemy żółty i niebieski kwadrat z pierwszej planszy, układamy je w przeciwległych rogach otworu na drugiej planszy i uzupełniamy czterema trójkątami. Komentujemy, że w takim razie otwór jest takiej wielkości (“ma takie pole” – jeśli dziecko zna już pojęcie pola) jak cztery trójkąty, niebieski kwadrat i żółty kwadrat razem
- odkładamy elementy na miejsce
- w rogach otworu na drugiej planszy układamy cztery trójkąty. Pozostałą część otworu wypełniamy czerwonym kwadratem wyjętym z pierwszej planszy. Komentujemy, że w takim razie otwór jest takiej wielkości jak cztery trójkąty i czerwony kwadrat razem
- Teraz możemy podsumować te obserwacje: skoro cztery trójkąty, żółty kwadrat i niebieski kwadrat wypełniają taką samą lukę jak cztery trójkąty i czerwony kwadrat razem, to żółty kwadrat i niebieski kwadrat muszą być razem mieć takie samo pole jak czerwony kwadrat. U młodszych warto mieć dodatkowe cztery trójkąty, żeby to zobrazować, układając z jednej strony żółty kwadrat, niebieski kwadrat i cztery trójkąty, z drugiej strony czerwony kwadrat i cztery trójkąty, a potem zabrać z obu miejsc po cztery trójkąty.
Znów od układanki do “prawdziwego” dowodu niedaleko – wystarczy zastanowić się, czemu elementy akurat w taki sposób pasują w otwór z drugiej planszy 🙂
No i jeszcze jedna ważna rzecz: ze “starszakami” spróbujcie wyciąć pewien trójkąt prostokątny i powtórzyć dowody dla niego (wycinając odpowiednie elementy). Jeśli się uda, to znak, że dowód został dobrze zrozumiany! 🙂
Gotowe portki czyli rewia mody 😉
Z tak zdobytą i utrwaloną wiedzą możemy dopiero brać się za obliczenia. Możemy wykorzystać zadania podręcznikowe, ale równie dobrze możemy sami je stworzyć. Jak? na przykład wykorzystując geoplan [kto nie ma, może użyć kartki w kratkę ;)]! Ot, wybierzmy sobie jakieś dwa kołeczki, rozepnijmy między nimi gumkę i naciągnijmy jedną jej część by utworzyła “pionowe” i “poziome” przyprostokątne. Jeśli geoplan jest dostatecznie duży, możemy też gumkami zaznaczyć kwadraty zbudowane na bokach trójkąta (wiecie, jak to zrobić na “ukośnym” boku?). Jakie są długości boków trójkąta? W tym “pionowym” i “poziomym” odczytamy to bez problemu. Pole największego kwadratu możemy obliczyć, sumując pola małych kwadratów. A długość przeciwprostokątnej – wyciągając pierwiastek z tego pola 🙂
Inna sprawa, że w takiej geoplanowej czy kratkowej wersji można też obliczyć pole dużego kwadratu korzystając z wzoru Picka.
Chcielibyście więcej opowieści o tym, gdzie przydaje się twierdzenie Pitagorasa? Bo wraca do nas jeszcze wiele, wiele razy, jeśli tylko lubimy wiedzieć “dlaczego” różne rzeczy mają się w matematyce tak, a nie inaczej 😉
























