Poprzednim razem badaliśmy kwadraty liczb. Dziś będziemy mocno korzystać z tamtych doświadczeń, więc gdyby cokolwiek było niejasne, zachęcam do powrotu do tamtego wpisu.
Co to jest ten pierwiastek?
Gdy obliczaliśmy kwadraty, chcieliśmy zbudować kwadrat o zadanym boku. Jego pole (to, z ilu kratek się składa) nazywamy kwadratem liczby. Mogłoby być odwrotnie, gdybyśmy mieli określoną liczbę kratek i chcieli sprawdzić, jak duży będzie bok kwadratu, który możemy z tych kratek zbudować. Takie działanie nazywamy właśnie pierwiastkowaniem.
To połączenie jest bardzo ważne i warto spokojnie je przećwiczyć na małych liczbach:
- kwadratem liczby 3 jest 9, więc pierwiastkiem z 9 jest 3,
- kwadratem liczby 5 jest 25, więc pierwiastkiem z 25 jest 5,
- kwadratem liczby 8 jest 64, więc pierwiastkiem z 64 jest 8,
- kwadratem liczby 1 jest 1, więc pierwiastkiem z 1 jest 1.
Ale jak te wartości obliczać? Przy niewielkich wartościach najłatwiej odwołać się do tabliczki mnożenia, a konkretniej liczb “na przekątnej” tabliczki. Spróbujmy jednak na chwilę wczuć się w dziecko, które nie ma jeszcze opanowanej tabliczki mnożenia (tak! takie dzieci też mogą obliczać pierwiastki!). Przypuśćmy, że chce obliczyć pierwiastek z 49. Najłatwiej zrobić to, układając odpowiedni kwadrat. Można próbować różnych rozmiarów metodą prób i błędów, ale żeby mieć pewność, że “trafimy” z rozmiarem, możemy zacząć od małego (np. o boku 1) i stopniowo go powiększać. Pamiętacie, jak? Wystarczy dokładać “zakrzywiony pasek” 😉
Warto przy tym albo obliczać wartość kolejnych kwadratów (tak długo, aż dojdziemy do 49), albo – jeszcze lepiej – przygotować sobie na początku 49 znaczków i układać, póki nam ich wystarcza.
Gdy pierwiastek jest liczbą kilkucyfrową
Nasz sposób działał bardzo sprawnie, dopóki w grę wchodziły niewielkie liczby. Jak jednak obliczyć pierwiastek na przykład z liczby 441 albo 676? Tutaj z pomocą przychodzą kolorowe znaczki, które wykorzystywaliśmy do układania kwadratów liczb kilkucyfrowych, oraz schematy kwadratów, które dzięki nim odkryliśmy.
Przypomnijmy sobie, jak wyglądał taki schemat dla kwadratu liczby dwucyfrowej:
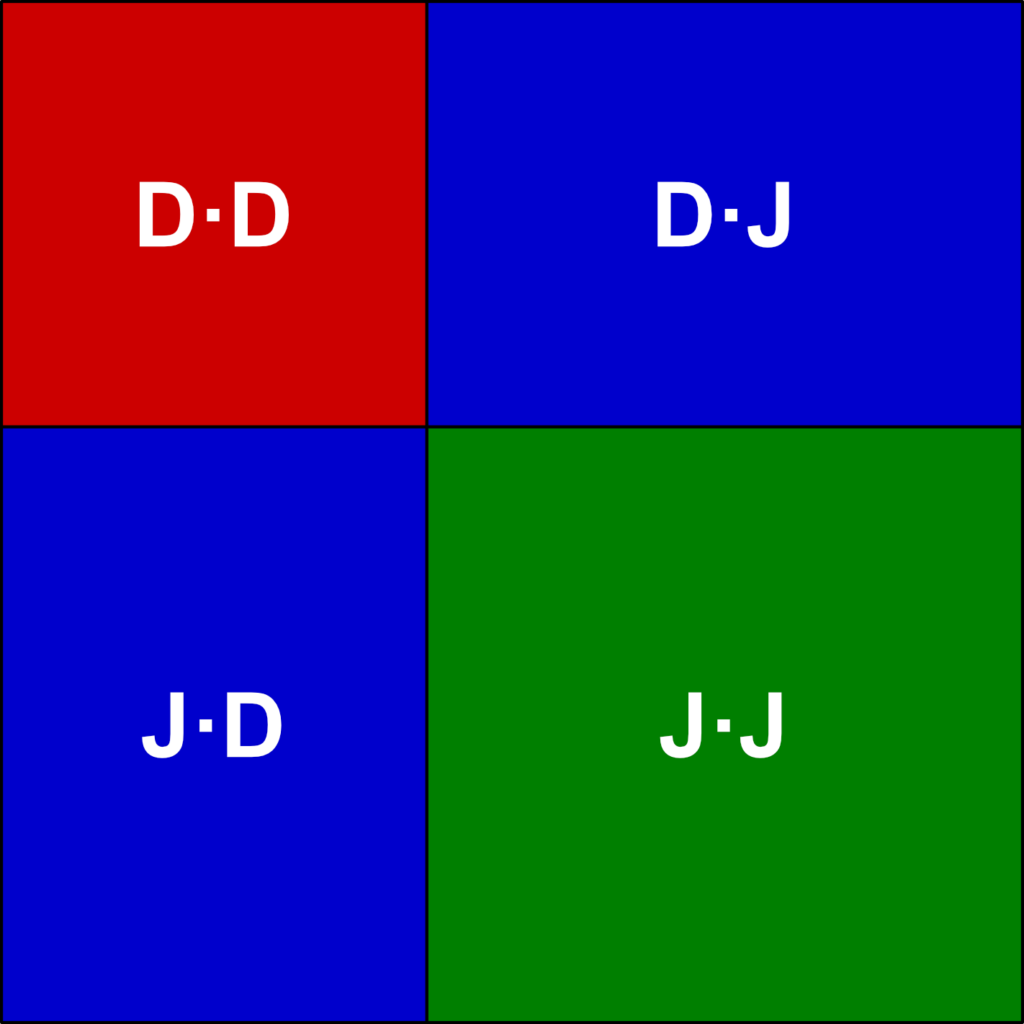
Pokażę na dwóch przykładach, jak wykorzystać go do obliczenia wartości pierwiastka.
Zacznijmy od liczby 441. Przygotowujemy 4 setki, 4 dziesiątki i jedną jedność. Spróbujmy ułożyć je według powyższego schematu. Niektórzy zobaczą od razu, jak będzie wyglądało rozwiązanie. Ale można też powoli (kolejne kroki znajdują się na zdjęciach poniżej) – zaczynając od czerwonych znaczków. Spróbujmy ułożyć jak największy czerwony kwadrat, będzie to kwadrat 2×2 (można zacząć od 1×1 i dołożyć “zakrzywiony” pasek”). Teraz będziemy dokładać “zakrzywione paski” z granatowych i zielonych znaczków, dopóki nam ich wystarczy. Pierwszy pasek układamy z 2 granatowych znaczków, 1 zielonego i kolejnych 2 granatowych. I to koniec, bo wykorzystaliśmy wszystkie znaczki!
Udało nam się ułożyć kwadrat o wartości 441. Ale jak odczytać wynik? Najłatwiej patrząc na kwadraty w naszym kwadracie 😉 Czerwony kwadrat 2×2 mówi nam o tym, że w wyniku będą 2 dziesiątki (bo czerwony kwadrat powstaje przez mnożenie dziesiątki razy dziesiątki). Zielony kwadrat 1×1 pokazuje, że wynik będzie miał 1 jedność. W takim razie pierwiastkiem z 441 jest 21.
Czy zawsze jest tak prosto? Aż tak łatwo nie zawsze, ale niewiele trudniej 😉 Trzeba tylko pamiętać o mocy rozmieniania znaczków. Popatrzmy na obliczanie pierwiastka z 676.
Zaczynamy od ułożenia czerwonego kwadratu. Na początek 1×1, rozbudowujemy go do 2×2, ale na 3×3 już nie wystarczy. Co w takim razie zrobić z pozostałymi dwiema setkami? Rozmienić! Wówczas będziemy mieć jeszcze do rozłożenia 27 dziesiątek i 6 jedności.
Zabieramy się teraz za układanie kolejnych “zakrzywionych pasków”, tym razem granatowo-zielonych. Przy pierwszym zużywamy 4 granatowe znaczki i 1 zielony (zostaje 23 granatowych i 5 zielonych). Przy drugim zużywamy 4 granatowe znaczki i 3 zielone (zostaje 19 granatowych i 2 zielone).
Na kolejny “zakrzywiony pasek” nie starczy nam już zielonych znaczków…? A jednak! Możemy przecież rozmienić jeden z granatowych znaczków (po zamianie mamy 18 granatowych i 12 zielonych). Teraz w kolejnych krokach:
- zużywamy 4 granatowe znaczki i 5 zielonych (zostaje 14 granatowych i 7 zielonych),
- zużywamy 4 granatowe znaczki i 7 zielonych (zostaje 10 granatowych znaczków),
- rozmieniamy granatowy znaczek (mamy 9 granatowych i 10 zielonych),
- zużywamy 4 granatowe znaczki i 9 zielonych (zostaje 5 granatowych i 1 zielony),
- rozmieniamy granatowy znaczek (mamy 4 granatowe i 11 zielonych),
- zużywamy 4 granatowe znaczki i 11 zielonych.
Wszystkie znaczki zużyte, pozostało odczytać wynik! Liczba dziesiątek w wyniku to bok czerwonego kwadratu, czyli 2. Liczba jedności to bok zielonego kwadratu, czyli 6. To oznacza, że pierwiastkiem z 676 jest liczba 26.
Jak wybrać schemat?
Mam nadzieję, że obliczanie pierwiastka, gdy mamy w ręce schemat, jest już jasne. Trudność może sprawiać jeszcze to, że schemat zależy od tego, ilucyfrowy wynik otrzymamy, a tego przecież nie wiemy! Skąd możemy się dowiedzieć?
Jeśli pierwiastkowana liczba jest jedno- lub dwucyfrowa, to pierwiastek będzie liczbą jednocyfrową, przecież schemat dla liczby dwucyfrowej “zaczyna się” od setek. Można to uzasadnić również inaczej: kwadrat najmniejszej liczby dwucyfrowej (czyli 10) jest równy 100, a więc jest już liczbą trzycyfrową.
Kwadrat liczby dwucyfrowej musi mieć co najmniej trzy cyfry, a maksymalnie…? Cztery! Gdy mamy liczbę pięciocyfrową (czyli co najmniej 10000), to pierwiastek będzie równy co najmniej 100.
Podobnie kwadrat liczby trzycyfrowej ma pięć lub sześć cyfr. I tak dalej…
Wielbiciele ogólnej zasady mogą ująć to tak: pierwiastek ma dwa razy mniej cyfr niż liczba, którą pierwiastkujemy, gdy ta liczba ma parzyście wiele cyfr. A jeśli ma ich nieparzyście wiele, to trzeba zaokrąglić w górę 🙂
A jeśli coś nam zostaje “reszta”?
Podobnie jak przy dzieleniu, zdarza się, że nie wszystkie znaczki uda nam się rozdzielić. Na przykład obliczając pierwiastek z 680 otrzymalibyśmy taki sam układ, jak przy pierwiastkowaniu 676, ale zostałyby nam jeszcze cztery jedności, które już nie starczają na kolejny “zakrzywiony pasek”. Co to oznacza?

To oznacza, że pierwiastek z 680 jest większy niż 26, ale mniejszy niż 27. Czy jesteśmy w stanie podać go dokładnie? W formie ułamka (zwykłego lub dziesiętnego) się nie uda, ale tego póki co nie uzasadnimy 😉 Możemy za to obliczyć kolejne cyfry po przecinku, ale do tego potrzebujemy schematu uwzględniającego ułamki dziesiętne i… kolejnego wpisu na blogu 😉





























