Obliczanie pól trójkątów to temat, który wydaje nam się odległy. W szkole wprowadzany jest w klasach 4-6 (zwykle w 5-tej klasie), a dla niektórych dzieci to ogromna strata! Spotkałam się z takimi uczniami, którzy matematykę “czują” bardzo geometrycznie. Dla nich pole prostokąta jest wyobrażeniem mnożenia (w metodzie Montessori zresztą doświadczają tego w czasie pracy z tabliczką mnożenia), a temat pól figur jest doskonałą zachętą do poznawania ułamków (we wzorach pojawia się tylko połowa, ale to dobry początek) czy mnożenia lub dzielenia dużych liczb.
Kiedy można wprowadzać pojęcie pola?
Odpowiedź mogłaby brzmieć jak zawsze: gdy dziecko będzie chciało spróbować 🙂 Jest jednak kilka kwestii, które umożliwiają realne zrozumienie tematu:
- umiejętność mnożenia (nie musi to być biegłe wykonywanie działań, ale zrozumienie, na czym mnożenie polega),
- pojęcie “połowy” (znów: dziecko nie musi znać ułamków zwykłych, a jedynie umieć intuicyjnie określić połowę niedużej liczby i rozumieć czym jest połowa odcinka),
- znać wzór na pole prostokąta (jeśli go nie zna, od niego rozpoczynamy pracę),
- rozumieć, że jednostką pola jest pole pewnego ustalonego kwadratu,
- znać pojęcie wysokości (można wprowadzić je na początku pracy z pomocą).
Jak wygląda pomoc i skąd ją wziąć?
Oryginalna pomoc zawiera figury wykonane z drewna, pomalowane na kolor żółty i podzielone na kratki o krawędzi 2cm. Wśród figur znajdują się:
- prostokąt o wymiarach 5×10 (wszystkie wymiary podaję w kratkach),
- równoległobok o podstawie 10 i wysokości 5, oraz dwie części, z których można ułożyć jednakowy równoległobok,
- trójkąt ostrokątny równoramienny o podstawie 10 i wysokości 10 oraz pięć części z których można ułożyć dwa kolejne takie trójkąty,
- trójkąt prostokątny równoramienny o przyprostokątnych długości 10 i dwie części do ułożenia takiego samego trójkąta,
- trójkąt rozwartokątny o jednym z boków przy kącie rozwartym długości 10 i wysokości 10 oraz trzy części do ułożenia jego kopii.
Pomoc możecie wykonać również samodzielnie. Opracowałam pliki PDF do wydruku zawierające prawie wszystkie elementy (oprócz równoległoboku i jego części, które znajdzie się w materiałach dotyczących pól czworokątów). Możecie je pobrać w wybranej wersji.
-
 Pola trójkątów0,00 zł
Pola trójkątów0,00 zł
Przy druku należy pamiętać o wyłączeniu skalowania. Elementy należy wycinać wzdłuż przerywanych linii. Warto zadbać o trwałość pomocy: można zalaminować wydruki przed pocięciem, wydrukować je na grubszym kartonie albo nakleić na gruby karton i wyciąć nożykiem introligatorskim.
Idealnym rozwiązaniem jest wykonanie elementów dwustronnych (na jednym ze zdjęć widać, że bez tego nie unikniemy odwrócenia na stronę “bez kratek”) – wśród plików znajdziecie również taką wersję.
Od czego zacząć?
W tym wpisie skupiam się na polu trójkąta, ponieważ istnieje doskonała pomoc opracowana przez Marię Montessori, która umożliwia poznanie wzoru na pole trójkąta. Obejmuje ona również pole równoległoboku, ale brakuje innych czworokątów, dlatego czworokąty (poza prostokątem) opiszę w oddzielnym wpisie z autorskimi rozwiązaniami. Warto rozpocząć prezentację pól od prostokątów, następnie omówić równoległoboki, a później inne figury (romby, trapezy, trójkąty) w dowolnej już kolejności. Jeśli jednak chcemy wykorzystać pomoc w konkretnym celu, nic nie stoi na przeszkodzie, by skorzystać tylko z konkretnego fragmentu pomocy.
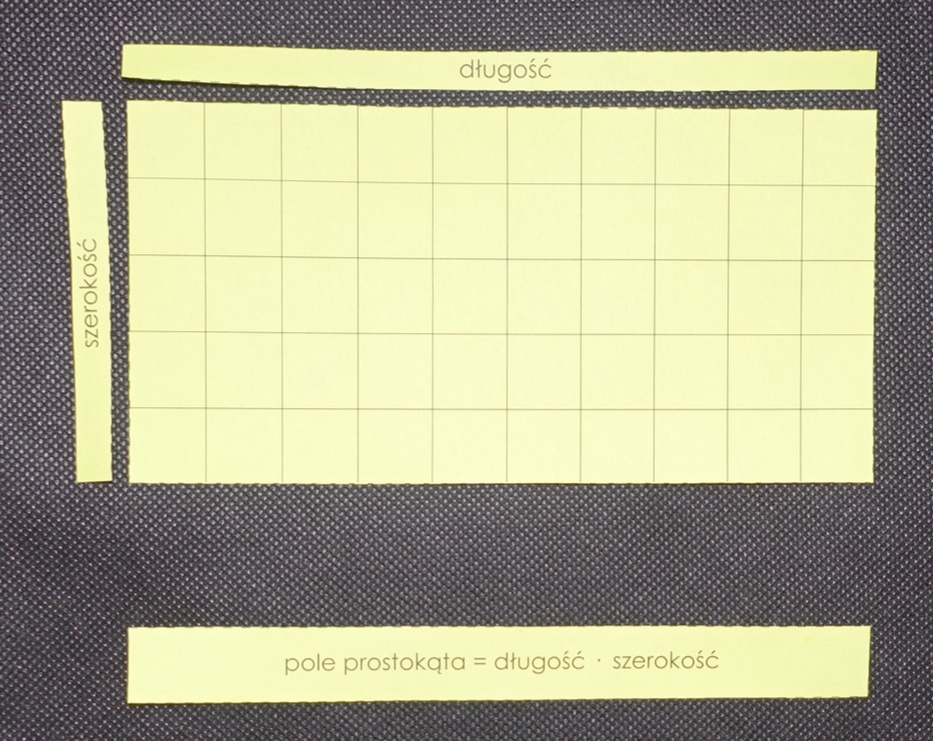
Jeśli dziecko nie pracowało wcześniej z polem prostokąta i równoległoboku, musimy zaprezentować mu prostokąt, pytając o to, jaką ma długość i szerokość (zwykle dzieci naturalnie określają je jako “10 kratek” i “5 kratek”). Następnie tłumaczymy, że będziemy chcieli policzyć pole prostokąta, czyli to, z ilu kratek się składa. Dziecko wybraną przez siebie metodą może policzyć, że jest ich 50. Część od razu zauważa, że jest to wynik mnożenia, a jeśli policzyło kratki “po jednej” lub innym sposobem, możemy mu to pokazać: “mamy 5 rzędów po 10 kratek, więc kratek jest 5 razy 10, czyli 50”. Obok odpowiednich boków umieszczamy podpisy “szerokość” i “długość”, a następnie pokazujemy dziecku zapisany słownie wzór na pole prostokąta: “Pole = szerokość x długość”.
Jeśli dziecko nie zna pojęcia wysokości trójkąta, możemy zaprezentować je w tym momencie. Prezentujemy wówczas poszczególne trójkąty i tłumaczymy, że aby obliczyć pole trójkąta będziemy potrzebowali zmierzyć coś więcej niż długości boków trójkąta. Musimy przygotować sznurek (proponuję sznurek grubości muliny, w kolorze czerwonym) z małym ciężarkiem na końcu, długości co najmniej 20 centymetrów. Następnie stawiamy trójkąt na jednym z boków (najlepiej tym “wzdłuż kratek”) i pytając “jak wysoki ten trójkąt?” przykładamy do wierzchołka znajdującego się na górze sznurek w taki sposób, by ciężarek swobodnie zwisał. Wydłużamy go na tyle, by ciężarek dotknął powierzchni, na której stoi trójkąt. Pokazujemy dziecku, że linia wyznaczona przez sznurek to wysokość trójkąta. Możemy też poprosić o odczytanie jej długości (“ile ma kratek”). Ważne by dziecko mogło zaobserwować, jak wygląda wysokość w różnych trójkątach – że może znajdować się we wnętrzu trójkąta, pokrywać się z bokiem, ale również być poza trójkątem.
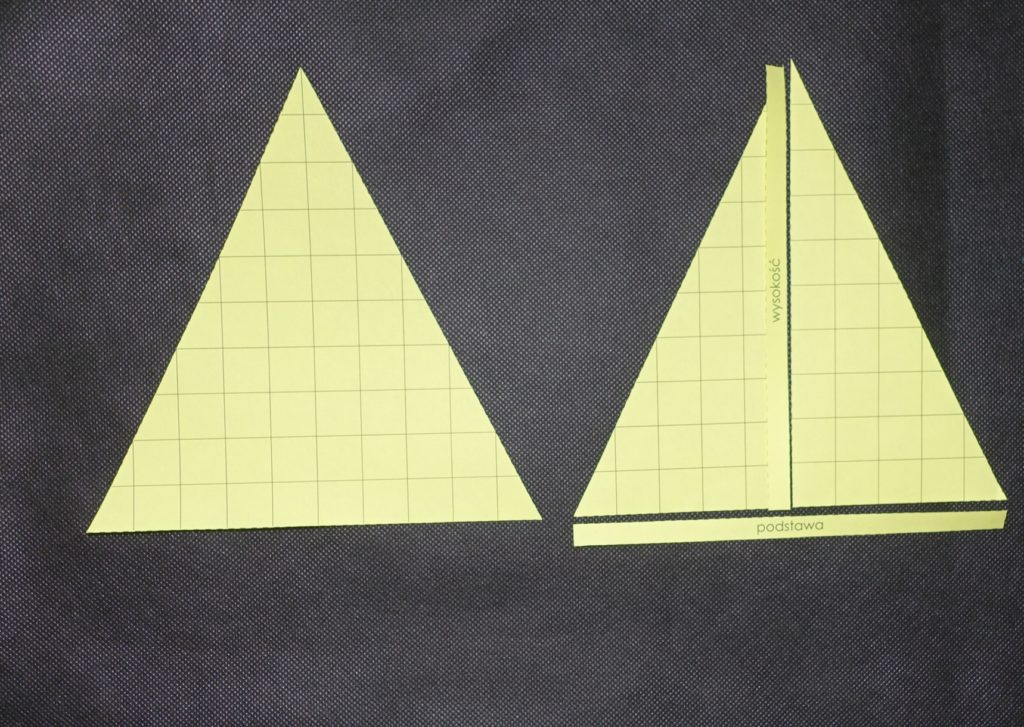
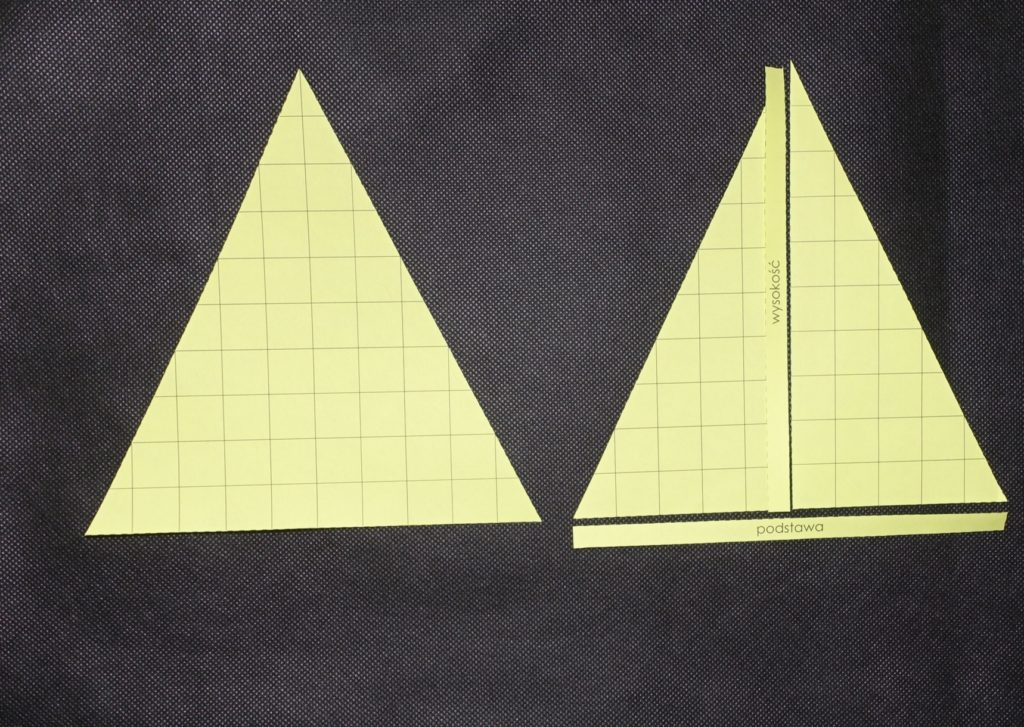
Prezentację pomocy związaną z wzorem na pole zaczynamy od czasu na to, by dziecko spróbowało na różne sposoby łączyć poszczególne elementy i manipulowało nimi. Doskonałą okazją do tego jest następujące ćwiczenie: prezentujemy dziecku trzy trójkąty i prosimy, by spróbowało ze wszystkich części ułożyć takie same trójkąty, przy czym jeden będzie miał dwie kopie, a pozostałe po jednej. Po zakończeniu tego zadania pomoc jest gotowa do prezentacji prowadzącej do poznania wzoru na pole trójkąta.
Jak pracować z pomocą?
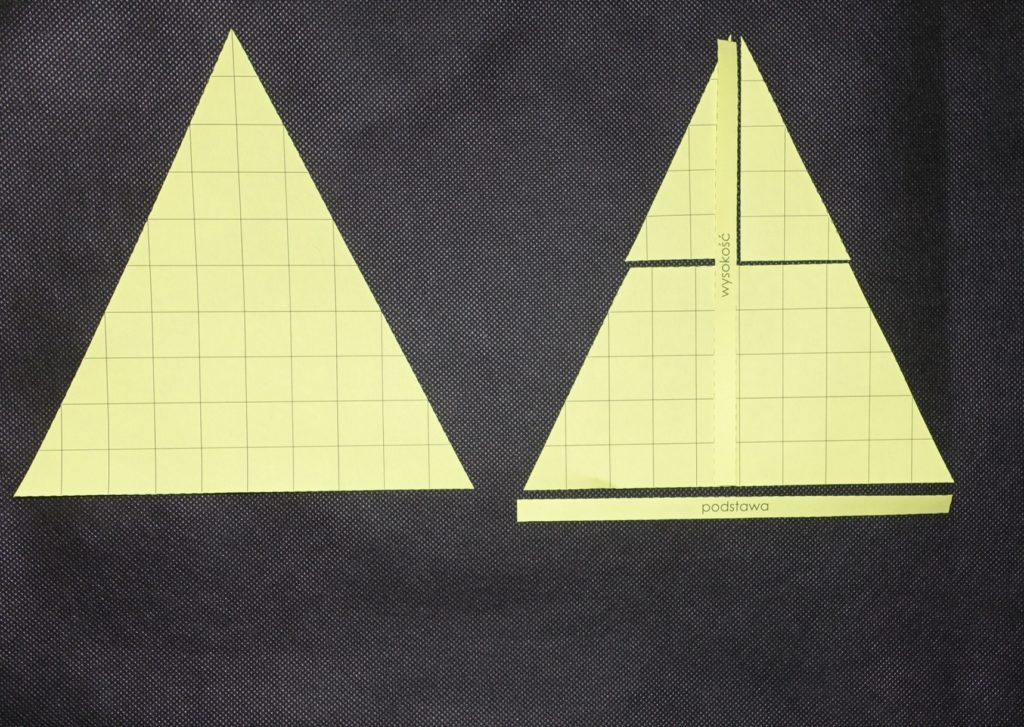
Zaczynamy od przypomnienia, czym jest pole (jest to “liczba kratek, z których składa się figura”) i zapytania dziecka, czy umie określić pole trójkątów, które znajdują się w pomocy. Rozmawiamy o tym, że nie jesteśmy w stanie określić tego od razu, ponieważ nie wszystkie kratki są “całe”. Zapowiadamy dziecku, że dzięki podzieleniu trójkątów na kawałki, zamienimy je w prostokąty.
Pracować będziemy w następującej kolejności: najpierw zajmujemy się trójkątem ostrokątnym ułożonym z dwóch części, potem trójkątem ostrokątnym z trzech części, następnie trójkątem prostokątnym i na koniec trójkątem rozwartokątnym.
Praca za każdym razem przebiega w jednakowy sposób:
- Wskazujemy podstawę i wysokość trójkąta, umieszczając przy nich podpisy z odpowiednimi słowami.
- Prosimy dziecko, by zwróciło uwagę, co dzieje się z podstawą i wysokością trójkąta w czasie przekładania elementów.
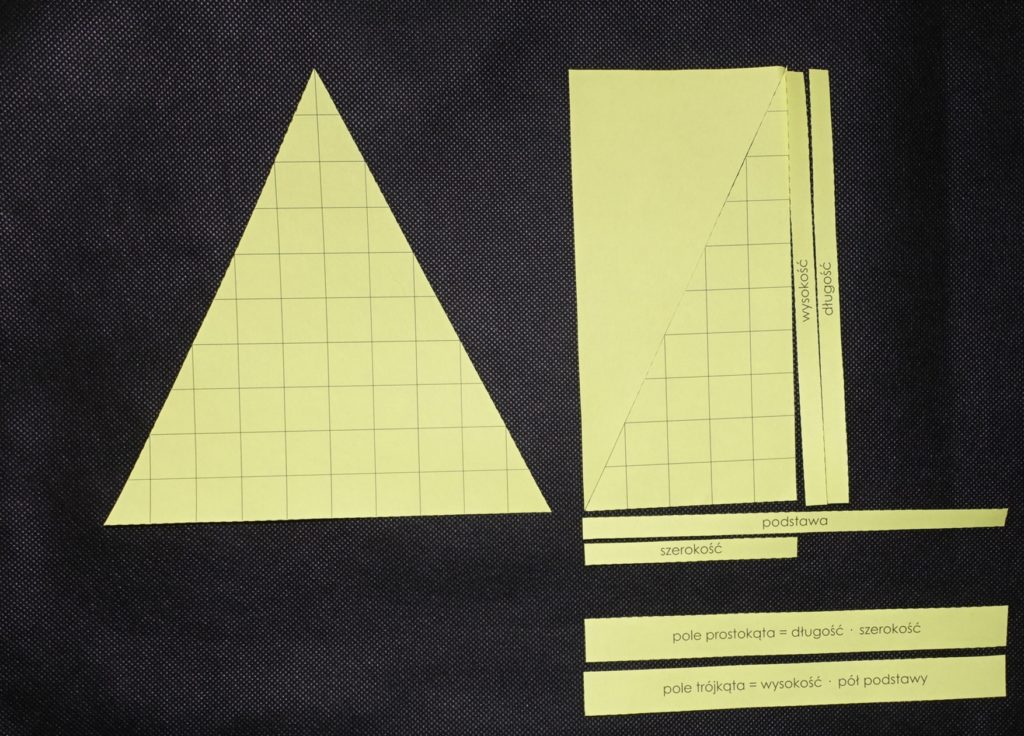
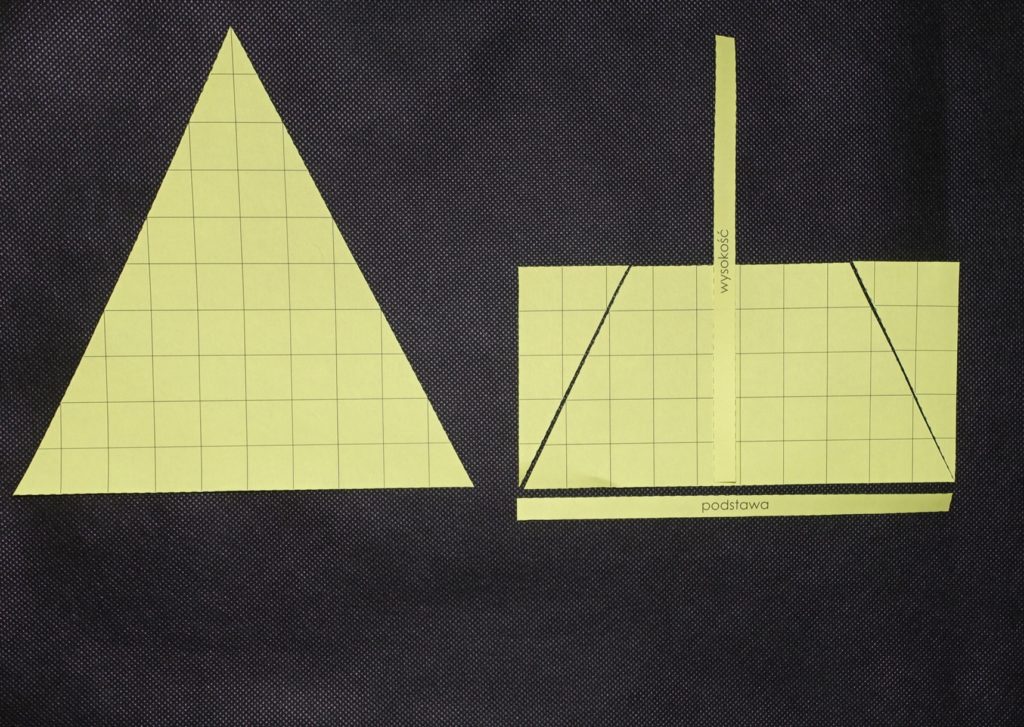
- Przekładamy elementy, tworząc prostokąt.
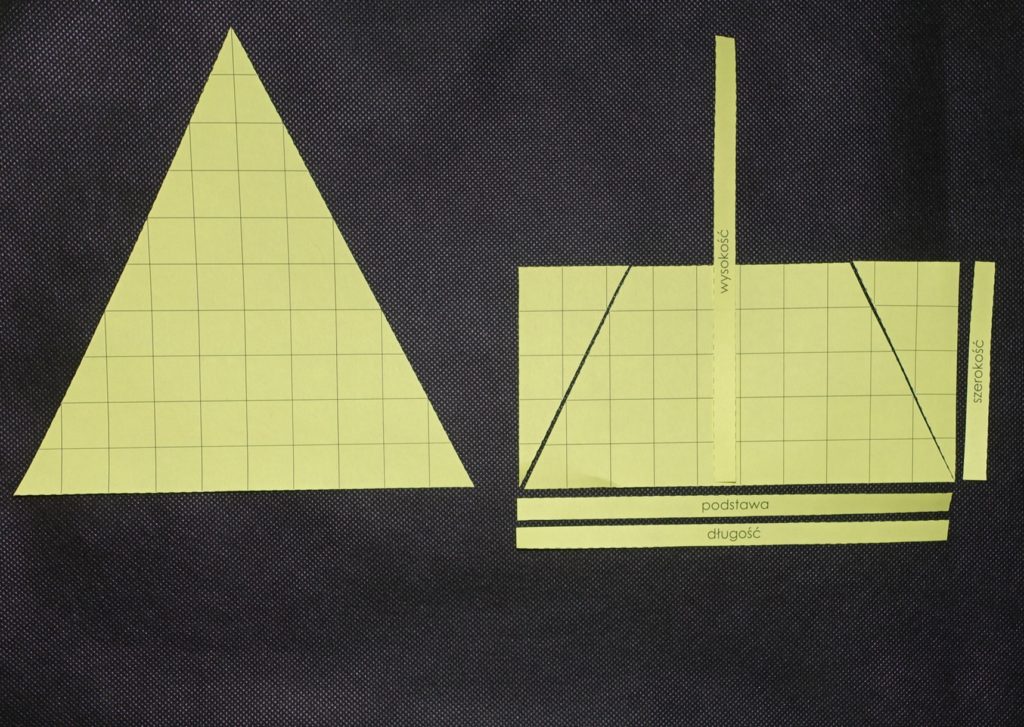
- Wskazujemy szerokość i długość prostokąta i pytamy dziecko o to, jakie są w porównaniu z podstawą i wysokością (zależnie od trójkąta długość prostokąta to podstawa/wysokość trójkąta, a jego szerokość to połowa wysokości/podstawy).
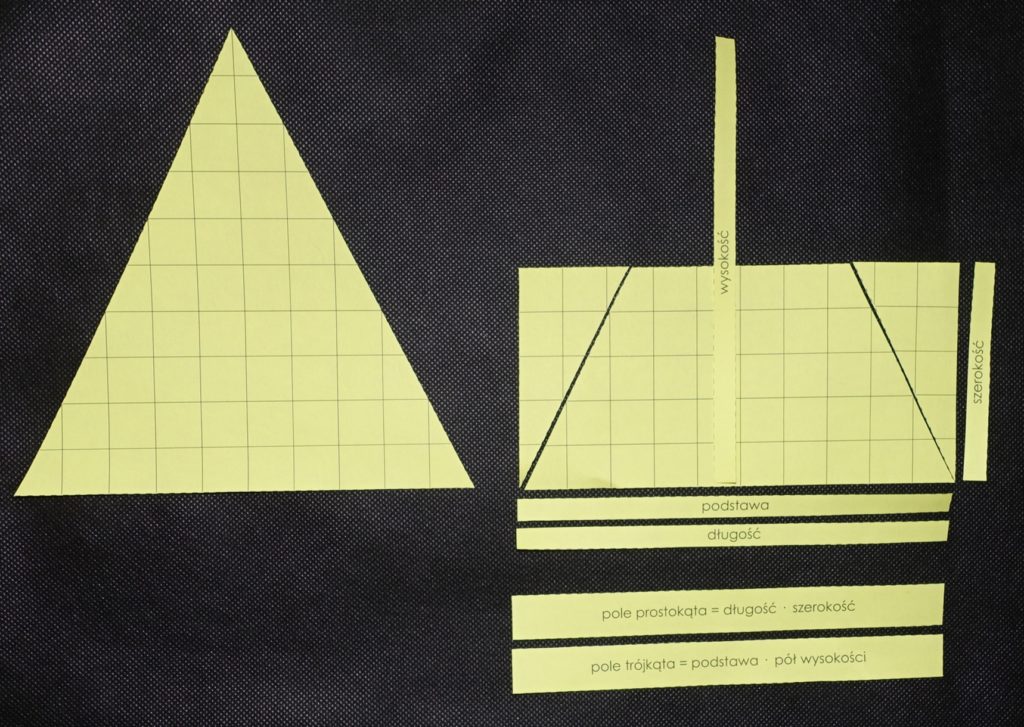
- Mówimy o tym, że pole prostokąta jest takie samo jak pole wyjściowego trójkąta. Przypominamy wzór na pole prostokąta, kładąc odpowiednią kartkę. Następnie mówimy o tym, że jeśli długość zastąpimy podstawą/wysokością trójkąta, a szerokość połową wysokości/podstawy, to otrzymamy wzór na pole naszego wyjściowego trójkąta i kładziemy odpowiednio zapisany wzór.
- Jeśli uważamy, że dziecko jest na to gotowe, możemy również pokazać abstrakcyjny zapis wzoru. Mówimy wówczas (kładąc odpowiednie podpisy i kartki z wzorami w czasie mówienia): “Jeśli podstawę trójkąta oznaczymy przez a i wysokość trójkąta oznaczymy przez h, to wzór na pole będzie wyglądał następująco: P = a · ½ h” (lub P = h · ½ a).
Po przejściu przez wszystkie trójkąty, warto podkreślić dziecku, że otrzymane dwa wzory dotyczą wszystkich rodzajów trójkątów i są dwoma sposobami na liczenie pola (często dzieci w pierwszej chwili myślą, że tylko jeden wzór może być prawdziwy).
Po zakończeniu takiej prezentacji można pogłębić temat na wiele sposobów:
- Jeśli dziecko potrzebuje nadal pracy na konkrecie, doskonałym ćwiczeniem jest rysowanie trójkątów na kratkowanym papierze (można wydrukować korzystając z przygotowanego pliku) i wycinanie ich. Potem możemy rozcinać je na fragmenty w taki sposób, by złożyć prostokąty lub od razu obliczać pola.
- Możemy wprowadzić metryczne jednostki pola: centymetr kwadratowy, milimetr kwadratowy, decymetr kwadratowy, metr kwadratowy. Wystarczy opowiedzieć o tym, że “kratka” może mieć różne rozmiary i niektóre z nich mają swoje specjalne nazwy 🙂
- Jeśli dziecko jest gotowe na spokojne przejście do abstrakcji, zachęcam do skorzystania z przygotowanych Baz o numerach 45-48 (trzy pierwsze dotyczą obliczania pól prostokątów i trójkątów w “kratkach”, ostatnia – na obliczaniu pól trójkątów w centymetrach kwadratowych).
-
 Baza 480,00 zł
Baza 480,00 zł -
 Baza 470,00 zł
Baza 470,00 zł -
 Baza 460,00 zł
Baza 460,00 zł -
 Baza 450,00 zł
Baza 450,00 zł -
 Papier w kratkę do badania pól0,00 zł
Papier w kratkę do badania pól0,00 zł










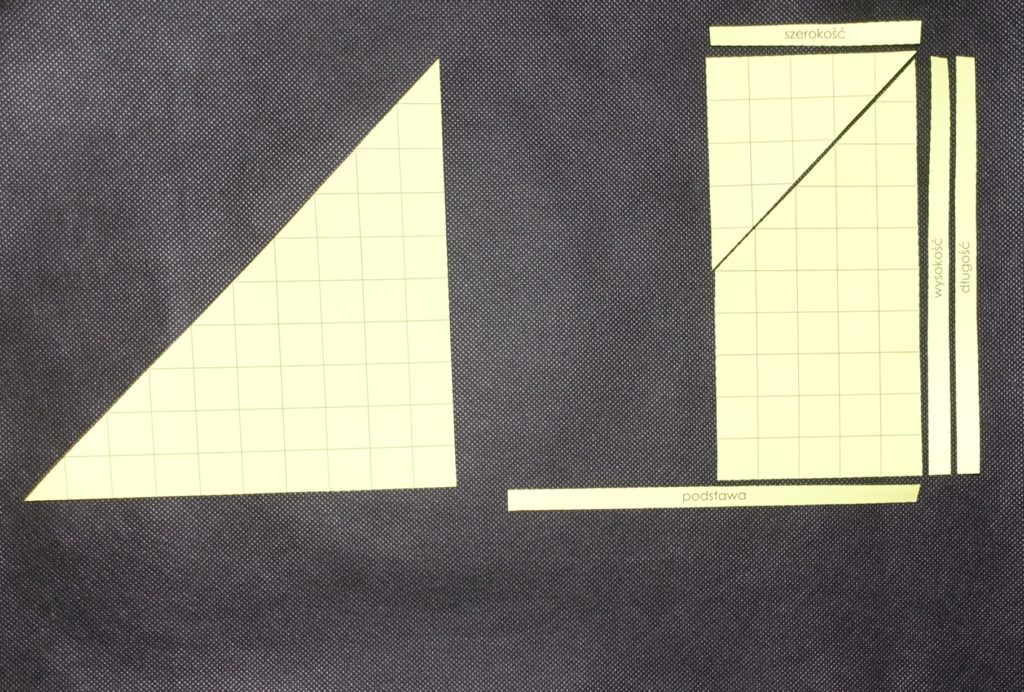













2 komentarze “Pola trójkątów”
Ulo, ta pomoc jest wspaniałą! Dziękuję Ci za nią i całą pracę, którą tutaj się dzielisz z innymi, buziak dzikapapieowka, Monika
Bardzo się cieszę i dziękuję za dobre słowo! A jednocześnie całą chwałę za tę pomoc (poza opracowaniem na komputerze) oddaję Marii Montessori 🙂 Zapraszam też do pól czworokątów, tam już więcej mojej twórczości 🙂