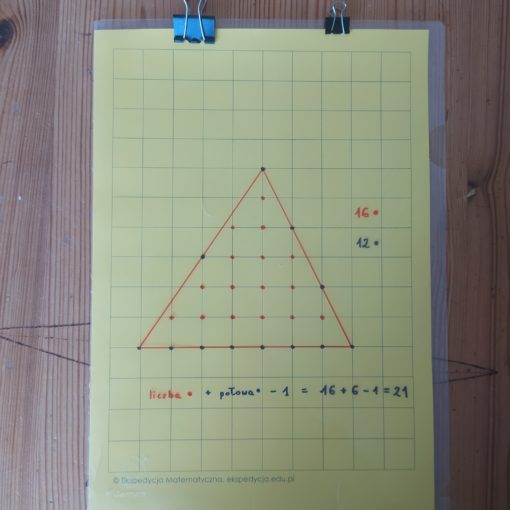
Chciałabym zaprosić was do zabawy w układanie parkietaży. Dziś skupię się na wielokątach foremnych, ale w ogólności można robić to za pomocą dowolnych płytek. O co chodzi? Chcemy pokryć całą płaszczyznę kafelkami w taki sposób, by na siebie nie nachodziły (mogą mieć wspólne tylko wierzchołki i boki) a jednocześnie by wypełniały całą płaszczyznę. W praktyce oczywiście przykryjemy tylko fragment płaszczyzny, ale często dostrzeżemy regularności, które przekonają nas, że możnaby układ powtarzać “w nieskończoność”.
My układamy najprostsze parkietaże z polskich klocków Reko. Tam, gdzie potrzebujemy wielokątów foremnych o większej liczbie wierzchołków, wykorzystaliśmy takie wycięte z papieru. Znajdziecie je razem z ułamkami (które też mogą się przydać) w poprzednim wpisie. Tam też możecie dowiedzieć się, jaka jest miara kątów w wielokątach foremnych i co mają ułamki do łączenia wielokątów w jednym wierzchołku. Jeśli jeszcze nie czytaliście, zajrzyjcie koniecznie!
Zabieramy się do układania – parkietaże foremne
Najprostszymi przykładami parkietaży są parkietaże ułożone z jednego rodzaju wielokątów (takie parkietaże nazywamy foremnymi).
Na początek spróbujmy z trójkątów, uda się doskonale (swoją drogą – można taki parkietaż wykonać nie tylko z trójkątów foremnych, możemy mieć dowolny trójkątny kształt płytki, ale to już na oddzielną opowieść, której namiastka jest we wpisie o trójkątach…). W każdym wierzchołku parkietażu, czyli w miejscach, gdzie łączą się wierzchołki kafelków, schodzi się po 6 trójkątów równobocznych, mówimy że jest to parkietaż stopnia 6.

Podobnie sytuacja wygląda z kwadratami – tutaj nikogo nie zaskakuje, że można pokryć płaszczyznę “w kratkę” (jest to parkietaż stopnia 4). Znowu można zaszaleć też z dowolnym innym czworokątem, ale póki co skupimy się na foremnych wielokątach…

Przy pięciokącie zaczynają się problemy. Trzy pięciokąty możemy bez problemu połączyć wierzchołkami, ale zostanie między nimi wąska szpara, w którą czwarty pięciokąt już się nie zmieści (nic dziwnego – kąt w pięciokącie foremnym jest rozwarty).

Czy to znaczy, że możliwości się skończyły…? Na szczęście nie. Są jeszcze sześciokąty, które doskonale pokrywają płaszczyznę, tworząc wzór znany np. z plastra miodu. W każdym wierzchołku parkietażu łączą się trzy sześciokąty, więc jest to parkietaż stopnia 3.

Kolejne wielokąty już nie przyniosą sukcesów. Dlaczego? Nie możemy połączyć trzech w jednym wierzchołku, bo mają kąt większy niż ten w sześciokącie foremnym. A dwa wielokąty foremne to za mało, by stworzyć wierzchołek parkietażu – mamy same kąty wypukłe.
Parkietaże półforemne
Czy to już koniec układania? Nic z tych rzeczy! Możemy spróbować połączyć różne rodzaje wielokątów foremnych i zobaczyć, co wydarzy się wtedy! Na początek ograniczymy się do tych możliwie regularnych parkietaży (półforemnych, nazywanych też archimedesowskimi – chcemy, żeby w każdym wierzchołku parkietażu “schodziły się” takie same wielokąty i to w takim samym układzie. Np. jeśli w jednym wierzchołku mamy trójkąt, kwadrat, sześciokąt i kwadrat, to w każdym innym ma być tak samo. Nie może być np. czterech kwadratów lub układu: trójkąt, dwa kwadraty i sześciokąt, w którym kwadraty są obok siebie, jeśli w pierwszym wierzchołku nie były.
No dobrze, ale jak szukać takich układów? Zastanówmy się najpierw, ile wielokątów musi schodzić się w jednym wierzchołku? Na pewno więcej niż 2 (bo wszystkie kąty są wypukłe, więc do kąta pełnego potrzebujemy więcej niż 2) i co najwyżej 6 (najmniejsze kąty wewnętrzne ma trójkąt równoboczny, 6 takich kątów tworzy już kąt pełny). W przypadku, gdy chcemy mieć 6 wielokątów, muszą to być same trójkąty, a taki parkietaż już mamy w swojej kolekcji. Dlatego skupimy się na parkietażach, w których w każdym wierzchołku schodzą się 5, 4 lub 3 wielokąty foremne.
Weźmy się do pracy i sprawdźmy, jakie parkietaże uda nam się znaleźć! Zaczniemy od poszukiwania odpowiednich zestawów wielokątów, które można złożyć w jednym wierzchołku. W drugim etapie sprawdzimy, czy każdy taki układ da się uzupełnić do regularnego pokrycia całej płaszczyzny (to wcale nie jest oczywiste!).
Parkietaże stopnia 5
Zacznijmy od parkietaży stopnia 5, czyli takich, w których w każdym wierzchołku schodzi się 5 wielokątów foremnych. Same trójkąty to za mało (do wypełnienia kąta pełnego potrzeba sześciu trójkątów). Spróbujmy użyć czterech trójkątów. Ich kąty, które spotykają się w wierzchołku parkietażu, mają łącznie 4·60°=240°. Pozostaje 120°, co doskonale można uzupełnić kątem sześciokąta foremnego. W ten sposób powstanie nam wierzchołek potencjalnego parkietażu, w którym schodzą się 4 trójkąty i sześciokąt.

Czy możemy ułożyć cały parkietaż z takimi wierzchołkami? Jak najbardziej, oto jego fragment:

Jeśli w wierzchołku pojawiłyby się trzy trójkąty, to ich “złączone” kąty razem miałyby 3·60°=180°. Zostaje nam wtedy jeszcze 180° do zapełnienia przez kąty dwóch innych wielokątów. Mogą to być dwa kąty proste, należące do kwadratów. Czy jest jeszcze jakaś możliwość? Nie, bo jeśli jeden z tych kątów byłby większy niż kąt prosty, to drugi musiałby być mniejszy, a mniejszy kąt pojawia się tylko w trójkącie, którego już mieć nie chcemy. Tym razem jednak otrzymaliśmy nie jeden, ale dwa potencjalne parkietaże, ponieważ trzy trójkąty i dwa kwadraty mogą być ułożone na dwa różne sposoby w wierzchołku (kwadraty obok siebie lub nie).
Czy w wierzchołku mogą pojawić się mniej niż trzy trójkąty? Kilka prób przekona nas, że to niemożliwie (gdy chcemy umieścić w nim łącznie pięć wielokątów). Możemy to uzasadnić: wtedy trzy pozostałe wielokąty miałyby kąty proste lub rozwarte, które razem mają co najmniej 270°. Pozostałe 90° nie wystarcza już na włożenie dwóch wielokątów, nawet jeśli mogą to być trójkąty.
Sprawdźmy jeszcze, czy każdy z dwóch uzyskanych układów wierzchołka daje się rozszerzyć do parkietażu? Chwila prób pokazuje, że tak! Na zdjęciach widać oczywiście tylko ich skończone kawałki, ale widać już pewną regularność, która przekonuje nas o tym, że da się je rozbudowywać.
Parkietaże stopnia 4
Analizę parkietaży stopnia 4 możemy poprowadzić podobnie, ale robi się to bardziej złożone. Niektórym łatwiej będzie myśleć o ułamkach. Ale gdzie tu ułamki? Przypomnijmy sobie, że kąt wewnętrzny w wielokącie foremnym to kąt półpełnego bez pewnej części (odpowiadającej danemu wielokątowi) kąta pełnego. Dokładny opis tej zależności można znaleźć w odpowiednim wpisie. Jeśli złożymy cztery takie kąty (mogą być z różnych wielokątów) w wierzchołku naszego parkietażu, to tak jakbyśmy składali cztery kąty półpełne bez pewnych ułamków kąta pełnego. Cztery kąty półpełne razem dają dwa kąty pełne, a my chcemy mieć tylko jeden! Stąd wniosek, że te “odbierane” ułamki kąta pełnego muszą złożyć się do całości.
Problem dobierania wielokątów zamienił nam się w zupełnie inny problem: jak przedstawić całość jako sumę czterech ułamków o liczniku 1 i mianowniku co najmniej 3, o tak:
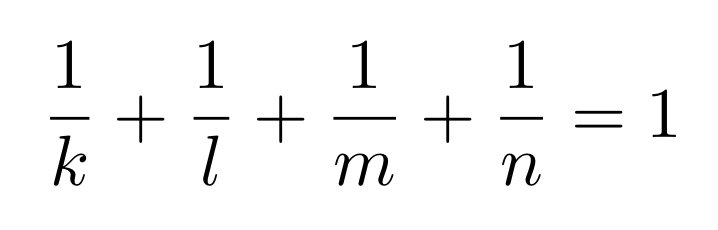
Czy to łatwiejszy problem? Nie, nadal ten sam 😉 Ale wyrażony w zupełnie innym języku. Na pewno daje większą łatwość w dokładnych obliczeniach – jeśli przyłożymy papierowe wielokąty i wszystko będzie pasować, to może się zdarzyć, że wcale nie pasują, ale “szpara” lub “nadmiar” są na tyle małe, że ich nie dostrzegamy. Każdy musi sam wybrać, czy woli tych dokładnych obliczeń dokonać na kątach, czy na ułamkach. Ja przedstawię rozumowanie na ułamkach.
Spróbujmy najpierw wykluczyć ułamek 1/3, czyli narzucić, by wszystkie ułamki miały mianownik co najmniej 4 (przypadek z ułamkiem 1/3 rozważymy później, oddzielnie). Wtedy każdy z tych ułamków to co najwyżej 1/4, czyli razem co najwyżej całość. A dokładnie całość pojawi się tylko w jednej sytuacji: gdy weźmiemy same ułamki 1/4. Taki układ ułamków odpowiada sytuacji, w której w wierzchołku parkietażu spotykają się 4 kwadraty – ten parkietaż już dobrze znamy 🙂
Teraz spróbujemy wziąć do naszej sumy jeden ułamek 1/3. Spróbujemy zastanowić się, ile może pojawić się ułamków 1/4? Na pewno nie mogą to być wszystkie trzy ułamki (1/3+1/4+1/4+1/4 to więcej niż 1). Jeśli spróbujemy wziąć dwa ułamki 1/4 to wyjdzie nam (z prostych obliczeń! choć można to również oszacować na materiale), że ostatni ułamek powinien wynosić 1/6. Doskonale – to znaczy, że w naszym parkietażu mogą w jednym wierzchołku spotkać się trójkąt, dwa kwadraty (obok siebie lub nie) i sześciokąt).
A co jeżeli jeden ułamek będzie równy 1/3 i dodatkowo tylko jeden ułamek będzie równy 1/4? Wówczas pozostałe dwa ułamki będą musiały mieć 1-1/3-1/4=5/12. To oznacza, że któryś z nich musi mieć przynajmniej połowę z 5/12, czyli 5/24. Ale to jest więcej niż 5/25=1/5. W takim razie bez drugiej 1/4 nam się nie uda.
Pozostało sprawdzić, czy możemy wziąć do naszej sumy ułamek 1/3, ale nie wykorzystywać 1/4? W takiej sytuacji trzy ułamki musiałyby mieć razem 2/3. Z drugiej strony każdy z tych ułamków to co najwyżej 1/5, razem dałyby co najwyżej 3/5, czyli… za mało! (żeby wiedzieć że za mało, trzeba porównać ułamki o różnych mianownikach, to też świetne ćwiczenie)
Ufff… Jeszcze jedna rzecz do sprawdzenia: czy w naszej sumie mogą pojawić się dwa ułamki 1/3? Pozostałe dwa ułamki musiałyby razem dać 1/3. To oznacza, że jeden z nich musi być równy co najmniej 1/6, a drugi co najwyżej 1/6. Oczywiście oba mogą być równe 1/6 – to daje nam potencjalny parkietaż, w którym w jednym wierzchołku schodzą się dwa trójkąty i dwa sześciokąty (ułożone “na zmianę” lub “parami”). A jeśli te dwa ułamki nie będą równe, to większy z nich musi być równy 1/4 lub 1/5, więc spróbujmy: sumę 1/3+1/3+1/4+…=1 możemy uzupełnić ułamkiem 1/12 (wtedy mamy dwa trójkąty, kwadrat i dwunastokąt – można je ułożyć w wierzchołku na dwa sposoby), ale do 1/3+1/3+1/5+…=1 pasuje 2/15 (policzcie!), którego nie da się zapisać z licznikiem o ułamku 1.
Trzy ułamki 1/3 w naszej sumie się nie pojawią, bo one same dałyby 1 i nic nie zostałoby dla czwartego ułamka 😉
Nie pozostaje nam nic innego, jak sprawdzić, czy każdy z uzyskanych układów rozszerza się do parkietażu. Okazuje się, że dwa układy możemy bez problemu rozszerzyć na całą płaszczyznę:
Pozostałych nie da się tak rozszerzyć do półforemnego parkietażu i dla wielu osób jest to spore zaskoczenie! Jednocześnie jest to dobra nauka, że nawet jeśli jakieś rozwiązanie wygląda na dobrą drogę, to ostatecznie może okazać się pułapką.
Układu z dwoma sąsiadującymi kwadratami, trójkątem i sześciokątem nie da się rozszerzyć, ponieważ kwadraty musiałyby układać się w pasy. Po jednej stronie takiego pasu pojawiłyby się na zmianę trójkąty i sześciokąty, ale… te sześciokąty miałyby wspólne wierzchołki, a przecież sześciokąty w naszym parkietażu miały się nie spotykać w wierzchołku.
Zobaczmy jeszcze, co się dzieje, gdy próbujemy do parkietażu półforemnego uzupełnić wierzchołek złożony z dwóch sąsiadujących sześciokątów i dwóch sąsiadujących trójkątów. W takiej sytuacji w drugim wspólnym wierzchołku naszych dwóch trójkątów musimy dołączyć dwa sześciokąty. Wtedy jednak stykają się one z wcześniejszymi sześciokątami, a pomiędzy nimi są pojedyncze trójkąty – a przecież sześciokąty i trójkąty w wierzchołkach parkietażu miały być obok siebie.
A co z układami z dwoma trójkątami, kwadratem i dwunastokątem? Jeśli chcemy, żeby trójkąty nie były obok, to powinniśmy otoczyć w parkietażu trójkąt kwadratem, dwunastokątem, kwadratem, dwunastokątem, … ups! Nie da się tak zrobić 😉 Jeśli za to trójkąty byłyby obok siebie, to próbując rozszerzać układ uzyskalibyśmy układ, w którym zetkną się trzy trójkąty… Spróbujcie sami!
Parkietaże stopnia 3
Pozostało nam przyjrzeć się parkietażom stopnia 3. Posługując się ponownie zależnością między kątami wielokątów foremnych i ułamkami możemy sprowadzić poszukiwania odpowiednich zestawów figur do następującego problemu: chcemy by suma trzech kątów półpełnych pomniejszonych o odpowiednie ułamki kąta pełnego dawała kąt pełny. Aby tak było, te trzy ułamki muszą dawać razem kąt półpełny. W takim razie szukamy możliwych sposobów na uzupełnienie za pomocą liczb nie mniejszych od 3 równości:
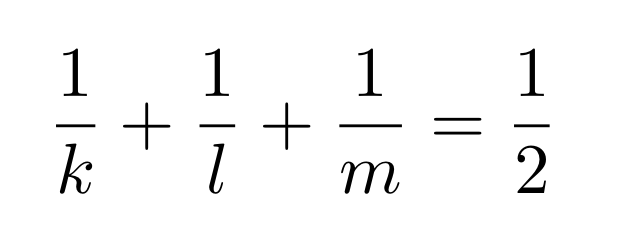
Na pewno możemy zrobić to za pomocą trzech ułamków 1/6 (to odpowiada parkietażowi z samych sześciokątów). Jeśli chcemy, by wielokąty były różne, to co najmniej jeden z ułamków będzie musiał być większy od 1/6, czyli równy 1/3, 1/4 lub 1/5.
Znów spróbujmy zacząć od ułamka 1/3. W naszej równości może pojawić się co najwyżej jeden taki ułamek, a wtedy pozostałe dwa muszą razem dawać 1/6. Łatwo zauważyć, że mogą to być dwa ułamki 1/12 (wówczas otrzymujemy potencjalny wierzchołek parkietażu, w którym schodzi się trójkąt i dwa dwunastokąty). W innej sytuacji jeden z ułamków musiałby być większy od 1/12 (ale mniejszy od 1/6), musimy więc sprawdzić, czy uda nam się uzupełnić naszą równość ułamkiem 1/7, 1/8, 1/9, 1/10 lub 1/11. Tak się składa, że wówczas trzeci ułamek (możemy go obliczyć wykonując odejmowanie od 1/6 naszego “kandydata”) byłby równy odpowiednio 1/42, 1/24, 1/18, 1/15 lub 5/66. Ostatnia opcja odpada (ułamka 5/66 nie przedstawimy w postaci z licznikiem 1), ale pozostałe dają nam cztery różne opcje na wierzchołek parkietażu:
- trójkąt, siedmiokąt i 42-kąt,
- trójkąt, ośmiokąt i 24-kąt,
- trójkąt, dziewięciokąt i 18-kąt,
- trójkąt, dziesięciokąt i piętnastokąt,
- no i znaleziony na początku układ z trójkątem i dwoma 12-kątami.
Jeśli w naszej równości nie pojawi się ułamek 1/3, to spróbujmy ułamka 1/4. Znowu w naszej równości może pojawić się co najwyżej jeden taki ułamek (dwa dawałyby już 1/2 i nic nie zostałoby dla trzeciego ułamka). Pozostałe dwa muszą sumować się do 1/4. Możemy uzyskać to dodając dwa ułamki 1/8 (to daje nam potencjalny wierzchołek parkietażu z kwadratu i dwóch ośmiokątów). W innych rozwiązaniach jeden z ułamków musiałby być większy od 1/8 (i jednocześnie mniejszy od 1/4), mamy więc możliwości 1/5, 1/6 i 1/7. Przy takich “kandydatach” trzeci ułamek musiałby być równy odpowiednio 1/20, 1/12 lub 3/28. Ostatnia możliwość “odpada”, uzyskaliśmy dwa kolejne zestawy wielokątów do jednego wierzchołka:
- kwadrat, pięciokąt i 20-kąt,
- kwadrat, sześciokąt i dwunastokąt,
- no i układ z kwadratem i dwoma ośmiokątami.
Pozostało nam sprawdzić możliwości, w których nie występuje 1/3 ani 1/4, pojawia się za to 1/5. Pozostałe dwa ułamki muszą wtedy dawać w sumie 1/2-1/5=3/10. W takim razie jeden z nich musi być równy co najmniej 3/20, a drugi – co najwyżej 3/20. Ten większy może być w takim razie równy 1/6 lub 1/5. Po obliczeniu trzeciego ułamka otrzymalibyśmy w tych sytuacjach odpowiednio 2/15 i 1/10. Tylko ta druga możliwość wchodzi w grę i odpowiadałaby wierzchołkowi parkietażu, w którym pojawiają się dwa pięciokąty i dziesięciokąt.
Łącznie uzyskaliśmy 10 możliwości (w tym jedna odpowiadająca parkietażowi foremnemu). Musimy jeszcze sprawdzić, który wierzchołek da się rozbudować do całego parkietażu. Poniżej zestawiam wszystkie możliwości – zielonym kolorem zaznaczyłam te, które dają nam parkietaż.
- trzy sześciokąty,
- trójkąt, siedmiokąt i 42-kąt,
- trójkąt, ośmiokąt i 24-kąt,
- trójkąt, dziewięciokąt i 18-kąt,
- trójkąt, dziesięciokąt i piętnastokąt,
- trójkąt i dwa 12-kąty,
- kwadrat, pięciokąt i 20-kąt,
- kwadrat, sześciokąt i dwunastokąt,
- kwadrat i dwa ośmiokąty,
- dwa pięciokąty i dziesięciokąt.
Najpierw możemy obejrzeć nowe parkietaże, które otrzymujemy:
A czemu pozostałe układy nie dadzą nam parkietaży? Powód jest w każdej sytuacji podobny: w każdym z nich pojawia się wielokąt o nieparzystej liczbie boków i dwa inne wielokąty. Te pozostałe wielokąty powinny leżeć wokół pierwszego “na zmianę” (żeby w każdym wierzchołku schodziły się trzy różne wielokąty). Ale przy nieparzystej liczbie boków nie da się tego zrobić! Tutaj próba otoczenia pięciokąta wierzchołkami, w których są po dwa pięciokąty i dziesięciokąt – widać, że “na dole” się nie uda.

Łącznie w całym artykule znaleźliśmy wszystkie 3 parkietaże foremne i 8 parkietaży półforemnych.
A co dalej?
Możemy spróbować połączyć różne rodzaje wierzchołków, otrzymując mniej regularne parkietaże. Pamiętajmy, że mamy już wszystkie możliwe rodzaje wierzchołków w parkietażach złożonych z wielokątów foremnych, więc nic tylko wybierać! 😉
Oczywiście można też zaszaleć z kształtami płytek – nie muszą to być wielokąty foremne!
A jeśli komuś znudziła się już przygoda na płaszczyźnie, można wyjść w przestrzeń. Trochę pisałam o tym w artykule o wielościanach foremnych. A na zachętę zostawiam jeden z efektów naszej pracy (powstał z jednego z parkietaży, po pomyśle dzieci: “a jak zamienimy sześciokąty na pięciokąty?”). Piękny, prawda?