Sporo już pisałam o mnożeniu pisemnym (tutaj i tutaj), dziś chciałabym pokazać jego kolejną odsłonę.
Spróbujemy zobaczyć, jak bardzo kwadratowe są kwadraty. Ale nie te geometryczne, tylko kwadraty liczb 🙂
Badanie kwadratów warto zacząć od kwadratów małych liczb. Świetnie nadają się do tego kolorowe liczby (szczególnie te połączone w łańcuchy, jeśli ktoś ma możliwość skorzystania z nich). Ja pokażę, jak wygląda taka praca z kolorowymi liczbami wydrukowanymi w domu. Większe kwadraty w pracowniach montessoriańskich oblicza się na tablicy perforowanej. Ja robię to na własnoręcznie wykonanych znaczkach.
-
 Kolorowe liczby0,00 zł
Kolorowe liczby0,00 zł -
 Znaczki – liczby naturalne0,00 zł
Znaczki – liczby naturalne0,00 zł
Zaczęliśmy od kwadratów liczb jednocyfrowych. Jak się za to zabrać? Możemy na przykład tak: wybieramy jedną z kolorowych liczb (polecam zacząć od innej niż 1 i 2) i dokładamy paski tak długo, aż postanie kwadrat. Jeśli będziemy układać paski liczby 5, to potrzebne nam będzie 5 pasków. Tak powstaje kwadrat liczby pięć. Teraz możemy zastanowić się, z ilu pól składa się ten kwadrat? Jest ich 25 (najlepiej liczyć je piątkami, przy okazji powtarzając wielokrotności), dlatego kwadrat liczby pięć jest równy dwadzieścia pięć. Łączy się to z polami prostokątów i mnożeniem – jeśli mamy je za sobą, warto do nich nawiązać.
Możemy powtórzyć to również z pozostałymi liczbami, otrzymując całą serię kwadratów:

A co się stanie się, jeśli będziemy chcieli zbudować kwadrat o boku większym od 10?
Osoby, które opanowały już mnożenie liczb kilkucyfrowych, mogą wyruszyć w dalszą podróż 🙂 Spróbujmy ułożyć kwadrat liczby 11, układając jedenastki za pomocą dziesiątek i jedynek. Łatwo zauważyć, że jedynek jest więcej niż 10, możemy więc część z nich zamienić na 10. Widać też, że jest ponad dziesięć dziesiątek, czyli cała setka! Spróbujmy więc zamienić nasze kolorowe liczby na znaczki. Jeśli to zrobimy, uzyskamy taki układ:

To dokładnie taki sam układ, co przy obliczaniu 11 razy 11. Przypadek? Wręcz przeciwnie, obserwowaliśmy już na mniejszych liczbach, że do obliczenia kwadratu liczby musimy pomnożyć ją przez samą siebie 🙂
Spróbujmy rozszerzyć znaczków do kwadratów kolejnych liczb. Łatwo dostrzec, że przy kolejnych zmianach boków musimy do kwadratu dołożyć “zagięty pasek”.

Podobnie będzie to wyglądało aż do liczby 19. Tyle, że czasem podliczanie będzie ciut bardziej złożone, będzie wymagało zamian znaczków (możemy wykonać je w głowie). Pokażę to na przykładzie kwadratu liczby 16. Ile jest równy?
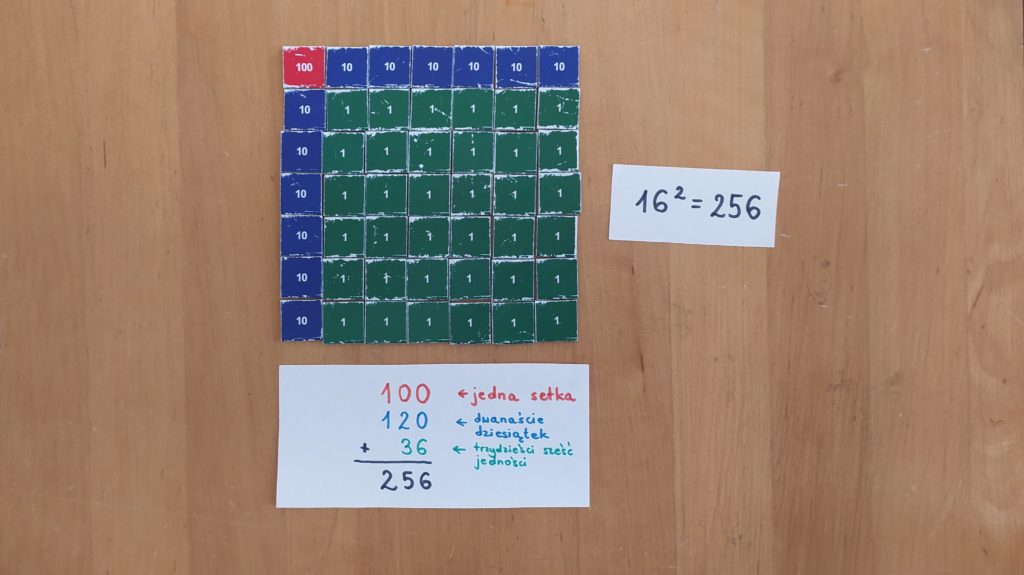
Mamy jedną setkę (czerwony znaczek). Do tego mamy dwanaście dziesiątek, czyli setkę i dwie dziesiątki. I do tego jeszcze trzydzieści sześć jedności, czyli trzy dziesiątki i sześć jedności. To razem setka, jeszcze jedna setka, dwie dziesiątki, jeszcze trzy dziesiątki i sześć jedności – razem 256. Jeśli dziecko biegle mnoży już przez potęgi liczby 10, to może również dokonać podliczenia w takiej formie, jak na zdjęciu (już bez opisów).
A co z kwadratami większych liczb dwucyfrowych?
Kwadraty liczb dwucyfrowych, czyli kwadraty z dwoma kwadratami
Gdy dojdziemy do kwadratu liczby 19, pojawia się chwila zawahania: co będzie przy 20? Możemy spojrzeć na to na dwa sposoby.
Pierwszy jest krótszy, ale nie zawsze oczywisty – jeśli dziecko samo na niego nie wpadnie, warto do niego dojść (o tym za chwilę). Kwadrat liczby 20 wygląda tak, jak mnożenie liczby 20 za pomocą znaczków, ot – cztery setki ułożone w kwadracik 😉
Drugie spojrzenie bierze się z dokładania “zagiętych pasków”. Spróbujmy dołożyć go do kwadratu liczby 19. Powstał nam całkiem pokaźny kwadrat, jeśli podliczymy składające się na niego znaczki, to też otrzymamy czterysta (sprawdźcie!). Możemy jednak coś zauważyć – po prawej stronie mamy w pierwszym rzędzie dziesięć dziesiątek, możemy wymienić je na setkę. Podobnie na dole pierwszej kolumny pojawiło się dziesięć dziesiątek, które zamieniamy na setkę. A ile zostało jedności? Dokładnie 100, też możemy zamienić je na setkę i uzyskujemy układ z drugiego sposobu.
Jak powiększyć ten kwadrat do kwadratu liczby 21? Potrzebny jest znów “zakrzywiony pasek”. Jaki dokładnie? Jeśli mamy wątpliwości, możemy wykonać mnożenie 21 razy 21 🙂 Powinniśmy otrzymać taki kwadrat, po podliczeniu znaczków w nim zawartych możemy odczytać, że kwadrat liczby 21 to 441.

Możemy w ten sposób budować kolejne kwadraty (bardzo polecam takie spokojne obliczanie kolejnych kwadratów z młodszymi dziećmi). Jeśli będziemy robić to dokładając “zagięte paski”, to przy pełnych dziesiątkach musimy dokonać zamian, by nie wykorzystywać zbyt wielu drobnych znaczków. Możemy również posiłkując się mnożeniem spróbować “przeskoczyć” do większej liczby, np. do kwadratu liczby 62. Efekt wraz z obliczeniem wartości możecie zobaczyć poniżej.
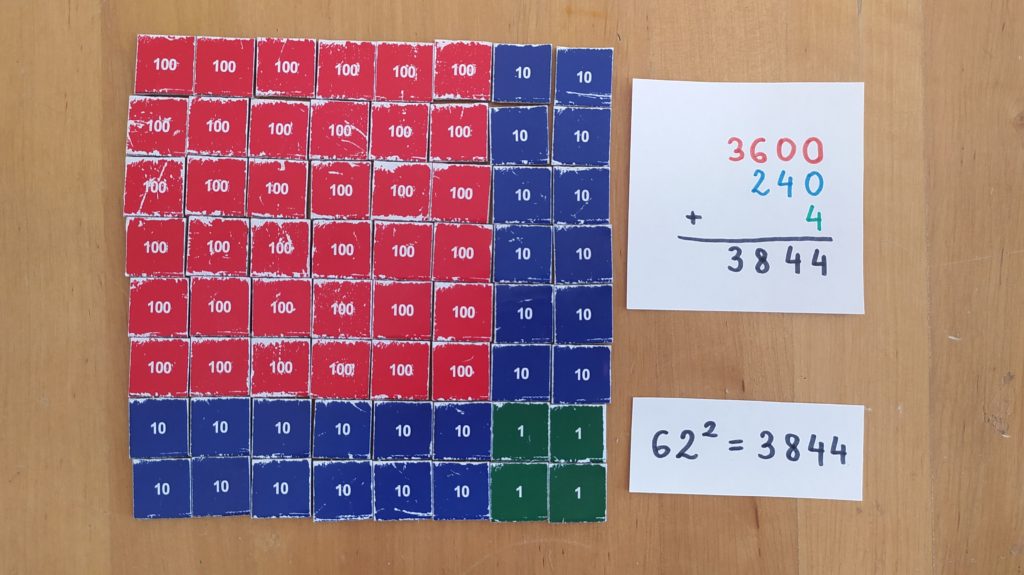
Czy widać już pewną zależność! Wierzę, że tak! Szczególnie jeśli ułożyliśmy tych kwadratów więcej. Ogólny wygląd kwadratu liczby dwucyfrowej jest taki:
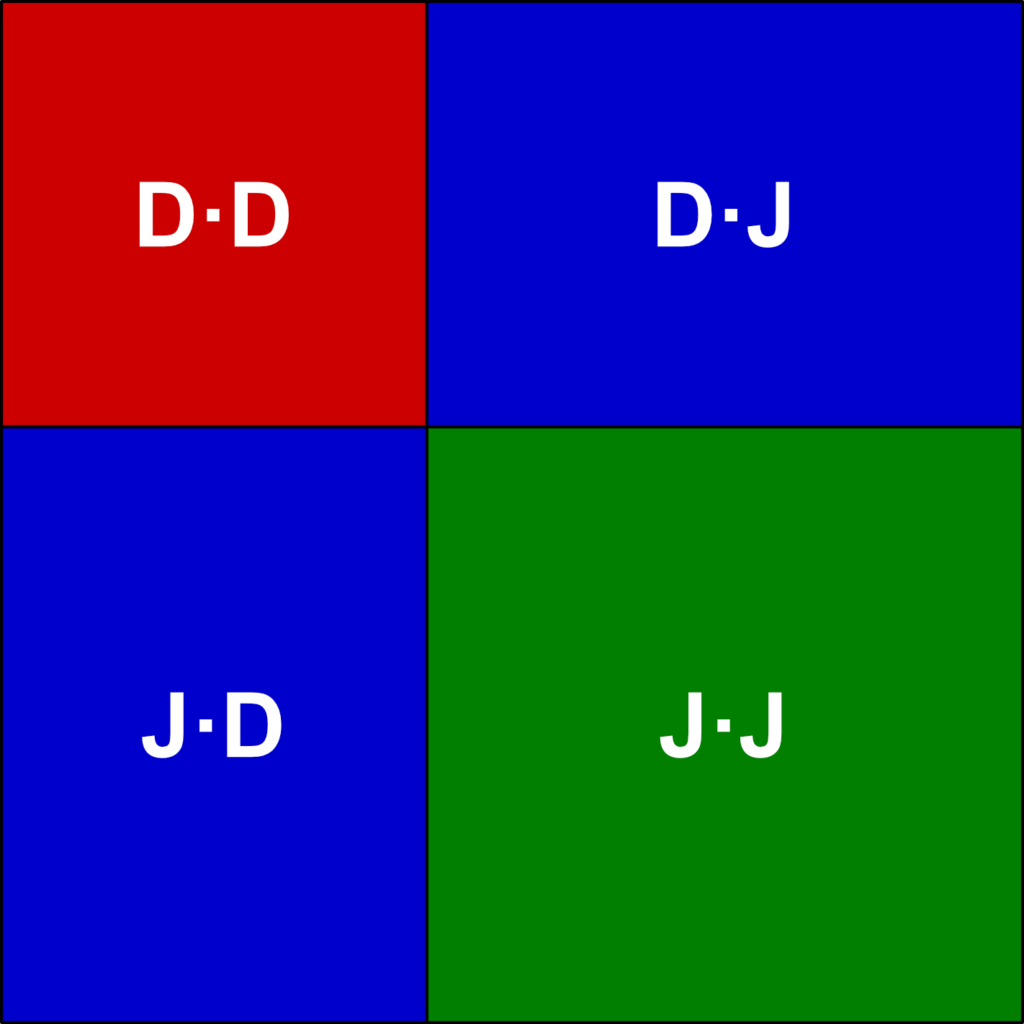
Dwie części (czerwona i zielona) są zawsze kwadratami, a ich rozmiar jest powiązany z liczbą dziesiątek i jedności w liczbie, której kwadrat układamy. Niebieskie części to prostokąty (czasem kwadraty, ale nie zawsze), które powstają z uzupełnienia czerwonego i zielonego kwadratu do dużego kwadratu 🙂 Litery oznaczają jedności (J), dziesiątki (D) i setki (S). Mnożenie podpowiada, jaki będzie rozmiar odpowiedniego prostokąta 🙂
W wyjątkowej sytuacji, gdy dwucyfrowa liczba nie ma jedności, zielonych i niebieskich części kwadratu nie ma.
Co z liczbami trzycyfrowymi?
Spróbujmy wykonać mnożenie 143 razy 143. Obliczając wartość wyznaczonych znaczków możemy posłużyć się mnożeniem pisemnym, ale możemy również zliczyć poszczególne rodzaje znaczków: mamy 1 dziesiątkę tysięcy, 4+4 tysięcy, 3+16+3 setek, 12+12 dziesiątek i 9 jedności. Ich łączna wartość obliczona jest na zdjęciu.

Spróbujmy ułożyć jeszcze jeden kwadrat, na przykład liczby 264.
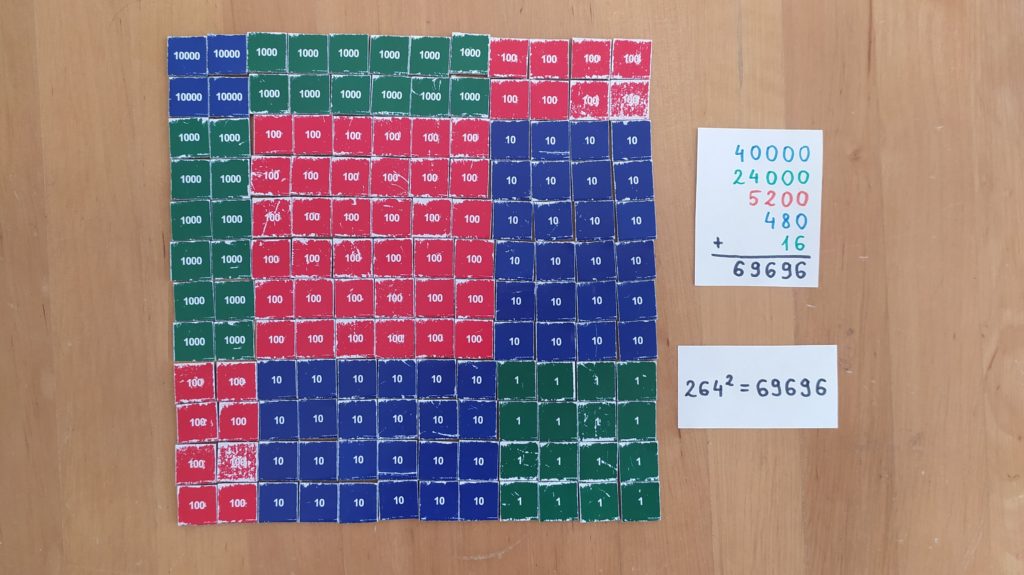
Spróbujmy jeszcze powiększyć ten kwadrat do kwadratu liczby 265. Znów wystarczy dołożenie “zagiętego paska”, zobaczcie:
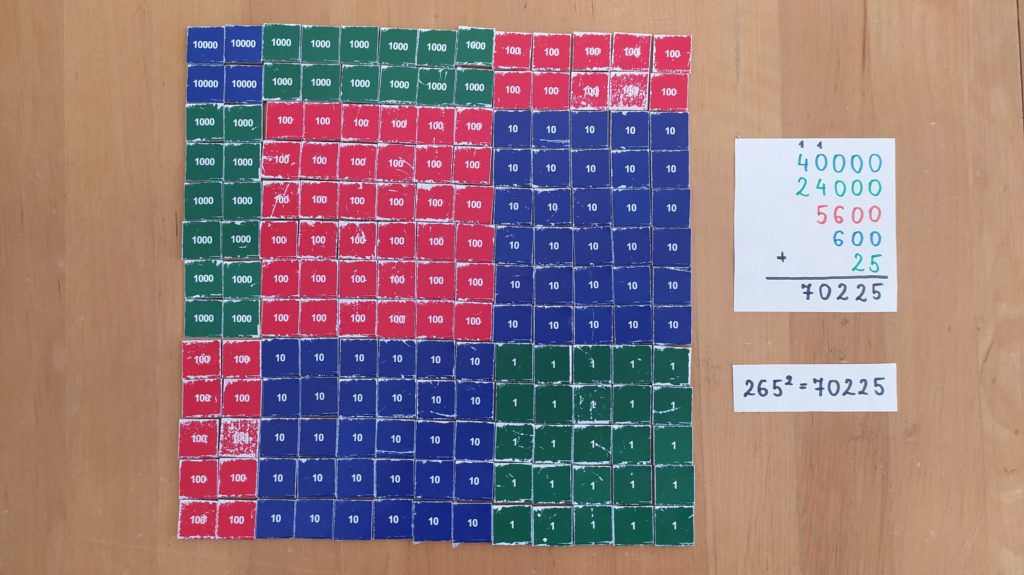
Czy widać już pewną zależność! Tak! (A jeśli nie, to możemy ułożyć więcej kwadratów ;))
Znów może zobrazować ją pewien schemat. Kryją się na nim trzy kwadraty oraz sześć prostokątów.
Podobnie jak poprzednio, jeśli cyfry w naszej liczbie się pokrywają, część z tych prostokątów również będzie kwadratami. A jeśli w naszej liczbie pojawi się cyfra zero, to części wierszy i kolumn nie będzie.
A co dalej?
Jeśli odkryliśmy już schematy kwadratów, możemy układać znaczki zgodnie ze schematem. Możecie pobrać takie schematy to wydruku:
Może wydawać się, że liczenie kwadratów w taki sposób jest sztuką dla sztuki – możemy przecież wykonać mnożenie pisemne. To prawda, ale ta metoda pokaże jeszcze swoją moc. Po pierwsze, już niedługo pozwoli nam na obliczanie pierwiastków z dużych liczb! Po drugie, będzie dobrą podbudową do nauki wzorów skróconego mnożenia 🙂 Ale o tym już innym razem… 😉 Czekacie?












