Wielokąty foremne i ułamki, czyli moc zależności

Jedną z najlepszych zachęt do badania wielokątów foremnych jest zmierzenie się z układaniem z nich przeróżnych parkietaży (czyli takich układów, w których wielokąty “nie nachodzą na siebie” (wspólne mają co najwyżej wierzchołki i boki), a jednocześnie szczelnie wypełniają płaszczyznę. Takie poszukiwania przedstawię w następnym wpisie, ale dziś chciałabym przedstawić piękną zależność, której można “dotknąć” dzięki montessoriańskim materiałom.

Będziemy wykorzystywać wielokąty foremne – mogą to być wielokąty z komody geometrycznej, klocki np. Connetix lub po prostu wielokąty wycięte z grubego papieru (im grubszy, tym wygodniej się układa – zachęcam również do naklejenia na tekturę introligatorską, kreatywną piankę itp.). Dziś nie będą jeszcze niezbędne jednakowe boki wielokątów, ale przy układaniu parkietaży już tak, możemy więc szykować materiał z myślą o przyszłości. Wielokąty do druku i ułamki można pobrać poniżej:

Co mają wspólnego wielokąty foremne i ułamki?

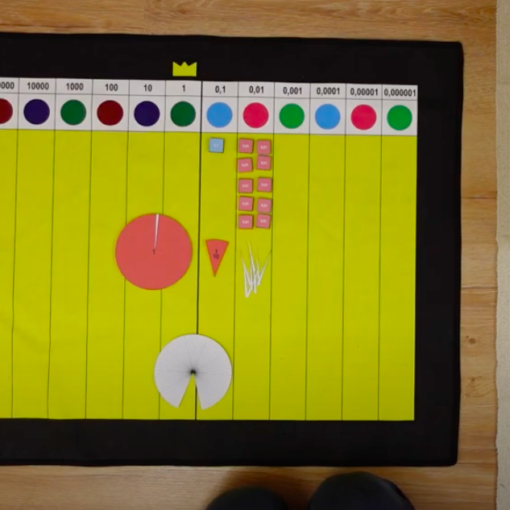
Przyjrzymy się dzisiaj temu, jakie miary mają kąty wewnętrzne wielokątów foremnych. Najłatwiej je określić przez podanie wartości kąta zewnętrznego. Jest to kąt utworzony przez bok wielokąta i przedłużenie sąsiedniego boku – razem z kątem wewnętrznym są kątami przyległymi, mają razem 180°. Jeśli macie pod ręką wielokąty foremne i ułamki zwykłe w postaci fragmentów kół, to koniecznie pozwólcie dzieciom sprawdzić samodzielnie, jakie te kąty są, poprzez przykładanie do wielokątów różnych ułamków.

Okazuje się, że kąt zewnętrzny w wielokącie foremnym to odpowiednia część kąta pełnego: kąt zewnętrzny trójkąta równobocznego to 1/3 kąta pełnego, kąt zewnętrzny kwadratu to 1/4 kąta pełnego, kąt zewnętrzny pięciokąta foremnego to 1/5 kąta pełnego itd.

Jeśli pracujemy z młodszymi dziećmi, wystarczy im to doświadczenie. Starszym możemy pokazać, skąd taka zależność się bierze.

Skąd to się wzięło?

Rozumowanie przeprowadzę na pięciokącie foremnym, ale można je powtórzyć na dowolnym innym wielokącie lub w ogólnej postaci (to ostatnie z dziećmi, które operują już wyrażeniami algebraicznymi).

Potniemy pięciokąt na pięć jednakowych trójkątów. Wystarczy pociąć go wzdłuż odcinków od “środka” do wierzchołków (istnienie takiego “środka” też wymaga uzasadnienia, ale intuicyjnie wynika to z dużej regularności wielokątów foremnych). Te odcinki mają jednakową długość, dlatego otrzymane trójkąty są równoramienne.

W takim razie kąty przy podstawie w naszym trójkącie są jednakowe. Oznaczam je kolorem zielonym. Kąt przy wierzchołku oznaczam kolorem czerwonym. Takie same kąty są we wszystkich pięciu trójkątach, również mogę je zaznaczyć.

Teraz możemy dostrzec dwie rzeczy: po pierwsze wiemy, że suma kątów naszego trójkąta to 180°, w takim razie do takiej wartości sumują się dwa kąty zielone i kąt czerwony. Jednocześnie dwa kąty zielone to kąt wewnętrzny naszego pięciokąta, więc kąt zewnętrzny daje w sumie z dwoma zielonymi kątami 180°. W takim razie kąt zewnętrzny pięciokąta foremnego ma taką samą miarę jak czerwony kąt! Jaka to wartość? Ano jedna piąta kąta pełnego – przecież pięć kątów czerwonych układa się na środku pięciokąta w kąt pełny 🙂

I już!

Do czego może nam się to przydać?

Naszą zależność wykorzystamy przy poszukiwaniu różnych parkietaży złożonych z wielokątów foremnych. Chcemy uzyskać różne zestawy wielokątów foremnych, których kąty razem zapełnią kąt pełny.

W jednym wierzchołku parkietażu może schodzić się 3, 4, 5 lub 6 wielokątów foremnych. Z dwiema ostatnimi opcjami “rozprawimy się” następnym razem. Podobnie jak ze szczegółową analizą dwóch pierwszych. Dziś chciałabym tylko pokazać wykorzystanie zależności i zostawić was z ułamkową zagadką 🙂

Przypuśćmy póki co, że szukamy czterech wielokątów, których kąty sumują się do kąta pełnego. Jak je znaleźć? Można oczywiście próbować, ale rozważanie wszystkich możliwości może być trudne, szczególnie ich dokładne sprawdzenie – przecież malutkiego błędu nie dostrzeżemy gołym okiem. Spróbujmy jednak wykorzystać naszą zależność: jeśli kąty wewnętrzne czterech wielokątów mają sumować się do kąta pełnego, to ich kąty zewnętrzne muszą również utworzyć kąt pełny. To dlatego, że każdy kąt wewnętrzny razem z odpowiadającym mu kątem zewnętrznym dają kąt półpełny – z czterech takich zestawów mamy dwa kąty pełne.

W takim razie szukamy czterech ułamków o liczniku 1 i mianowniku co najmniej 3 (taką częścią kąta pełnego są kąty zewnętrzne naszych wielokątów), które sumują się do 1. Zachęcam was do poszukania takich zestawów i zobaczenia, czy kąty odpowiednich wielokątów foremnych tworzą razem kąt pełny. Gdybyście znaleźli np. sumę 1/3+1/4+1/4+1/6, to możecie sprawdzić, że trójkąt, dwa kwadraty i sześciokąt doskonale pasują do wierzchołka parkietażu.

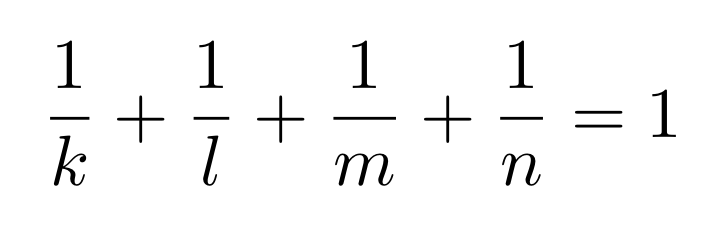
Bardzo podobną ułamkową zagadkę możemy ułożyć w sytuacji, w której w jednym wierzchołku mają złączyć się trzy wielokąty. Ich kąty wewnętrzne mają utworzyć kąt pełny. Za to każdy kąt wewnętrzny razem z odpowiadającym mu kątem zewnętrznym tworzą razem kąt półpełny. W takim razie trzy kąty wewnętrzne i trzy kąty zewnętrzne naszych wielokątów dają razem półtora kąta pełnego. W takim razie trzy kąty zewnętrzne muszą razem dawać kąt półpełny. Stąd uzyskujemy drugą zagadkę:

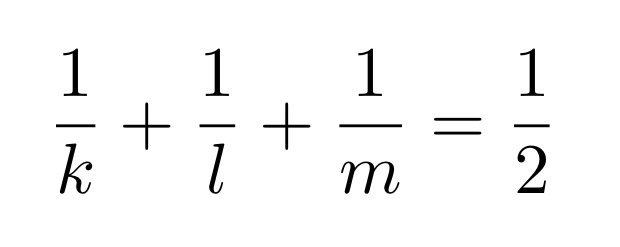
Młodsi mogą poszukać rozwiązań obu zagadek korzystając z konkretu (tu potrzebna jest odrobina ostrożności – małe błędy mogą nie zostać dostrzeżone, ale do prób jak najbardziej taka metoda się sprawdzi). Starsi mogą spróbować dokonać pełniejszej analizy, uporządkować możliwe przypadki, sprawdzić je za pomocą obliczeń. Mój opis, jak może to wyglądać krok po kroku, już w następnym wpisie 🙂