Czy ułamki zwykłe są faktycznie zwykłe?

Nazwa myląca i niepozorna. Ot, takie “zwykłe” ułamki. A mogą stać się okazją do wielu wspaniałych zaskoczeń! Chciałabym w serii wpisów pokazać, jak można je wprowadzać (już od przedszkola) i jakie elementy wiedzy z innych obszarów matematyki są potrzebne do zdobycia kompletu umiejętności dotyczących ułamków zwykłych.

Montessoriański “konkret”

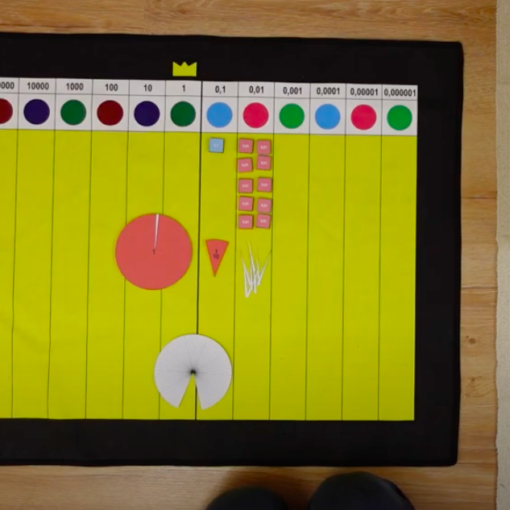
Montessoriański materiał do ułamków zwykłych składa się z czerwonych kół, niektóre są pocięte na wycinki. Całe koło odpowiada jedności, a w pozostałych przegródkach znajdują się części drugie (połowy kół), części trzecie, itd. aż do części dziesiątych. W każdej przegródce jest zwykle tyle części, by można było złożyć z nich pięć całości (5 całych kół, 10 części drugich, 15 części trzecich, 20 części czwartych itd.).

Jeśli nie macie takiego materiału, możecie wykonać go w domu. Opis wykonania znajdziecie w oddzielnym wpisie.

Również przy pomocach dostępnych w sprzedaży warto zwrócić uwagę na grubość ułamków: najlepsze są te w metalowych ramkach (dają większe możliwości na wczesnym etapie wprowadzania, chociaż do dalszych ćwiczeń mają zbyt mało części) lub grube plastikowe (wystarczające do wszystkich proponowanych przeze mnie ćwiczeń). Nie polecam tych cienkich – koszt jest spory, a użytkowanie w praktyce bardzo słabe.

Ułamki wokół nas

Wprowadzając ułamki bardzo lubię pokazywać ich związek z życiem – czasami po prostu potrzebujemy podzielić jedność. Możemy to zrobić choćby na przykładzie jabłka, rozmawiając z dzieckiem o tym, co możemy zrobić, jeśli mamy tylko jedno jabłko, a kilka osób chciałoby je zjeść. Pomysłów może być dużo, ale jest spora szansa, że jednym z nich będzie podzielenie jabłka. Warto zaangażować zmysły i poprosić dziecko, żeby to zrobiło! A kiedy już skosztujemy jabłko, możemy powiedzieć o tym, że ułamki do tego właśnie służą – mają pozwolić nam na opisywanie liczbą nie tylko całości, ale też jej części. W matematyce podział przeprowadzamy na jednakowe części – w rzeczywistości jest to w zasadzie niemożliwe do wykonania (ale możemy się starać, dbając o dużą precyzję).

• 

• 

Wprowadzenie materiału

Przy wprowadzaniu materiału przygotowujemy jedno całe koło i po jednym kole podzielonym odpowiednio na dwie, trzy, cztery, itd. części. Liczbę kół dostosowujemy do możliwości dziecka – dla niektórych części drugie i trzecie będą wystarczającą lekcją na początek, inne przyswoją bez problemu wszystkie części aż do części dziesiątych. Prezentujemy całe koło przypominając, że “to jest jedność”. Następnie rozmawiamy z dzieckiem o tym, na ile części jest podzielone następne koło i komentujemy, że “ponieważ jedność jest podzielona na dwie części, każda z tych części nazywa się jedna druga“.

Jednocześnie z nazwą wprowadzamy zapis ułamka: na karteczkach piszemy “jedna druga” na każdej z części umieszczamy jej podpis. Warto zrobić to nawet jeśli części są już podpisane – to dlatego, że wówczas dziecko widzi kolejność wykonywania zapisu i łączy zapisane cyfry z wypowiadanymi słowami (mówimy “jedna” pisząc cyfrę 1, następnie piszemy kreskę, a na koniec piszemy cyfrę 2 mówią “druga”).

Podobnie wprowadzamy kolejne części: zaczynając od określenia, na ile części zostało podzielone koło, poprzez nazwanie, aż do zapisu.

Utrwalenie nazewnictwa (i oznaczenia symbolicznego) warto zrobić zgodnie z montessoriańską lekcją trójstopniową – prezentację mamy za sobą, pora więc na identyfikację (prosimy dziecko o wykonanie różnych czynności z nazwanymi przez nas częściami) i na końcu przywołanie nazw z pamięci (to my wybieramy części, a dziecko je nazywa/podpisuje).

Ważną sprawą są też inne nazwy ułamków, takie jak połowa i ćwierć. Dziecko prawdopodobnie je zna – jeśli tak jest, to warto po wprowadzeniu nazewnictwa, w ramach jego utrwalania, nawiązać do tego – która z tych części to połowa? która z tych części to ćwierć? Po ich odnalezieniu tłumaczymy, że “połowa” i “jedna druga” to dwie różne nazwy tej samej liczby, tak samo jak “ćwierć” i “jedna czwarta”. Jeśli dziecko samo zapyta wcześniej, nie bójmy się mu tego wyjaśnić!

Ważne jest też pokazanie dziecku, że ułamek nie zawsze oznacza część koła. Może to być część jedności przedstawionej w inny sposób. Doskonale możemy zrobić to, dzieląc na odpowiednią liczbę części kwadrat (zawsze możemy zrobić to “na paski”, ale przy niektórych ułamkach są też inne możliwości, które warto pokazać). To dobre ćwiczenie utrwalające i przypominające ważną własność – jeśli chcemy opisać część za pomocą ułamka, całość musi być podzielona na jednakowe części. Jeśli dziecko ma problem z abstrakcyjnym myśleniem, możemy jednak zostać przy kole, sprawę ułamka “czegoś” pozostawiając na dalszy etap nauki.

A jeśli części jest więcej…?

Jeśli dziecko opanowało nazwy poszczególnych części, możemy przejść do kolejnego etapu – poznawania ułamków o liczniku innym niż jeden. Na początku przygotowujemy po jednym kole z każdego rodzaju części. Prosimy dziecko o podanie kilku jednakowych części, na przykład o “dwie części trzecie”. Układamy je razem, tworząc spójny wycinek koła i mówimy o tym, że taka część koła, to “dwie części trzecie”, dlatego nazywamy go “dwie trzecie”. Jednocześnie wprowadzamy zapis.

W podobny sposób prezentujemy dziecku inne ułamki, np. 2/5, 3/4, 7/10. Po jakimś czasie, dziecko powinno przejąć inicjatywę. Gdy widzimy, że zasada nazywania i zapisywania ułamków jest dla dziecka jasna, możemy zorganizować dalszą pracę, proponując dziecku rozwiązanie Bazy numer 56, dotyczącej układania ułamków do ich zapisu.

Nie przygotowałam bazy “odwrotnej”, w której na podstawie materiału dziecko nazywa i zapisuje ułamek, ponieważ nazwanie części na podstawie rozmiaru jest dla dziecka dostępne tylko, gdy może manipulować poszczególnymi częściami.

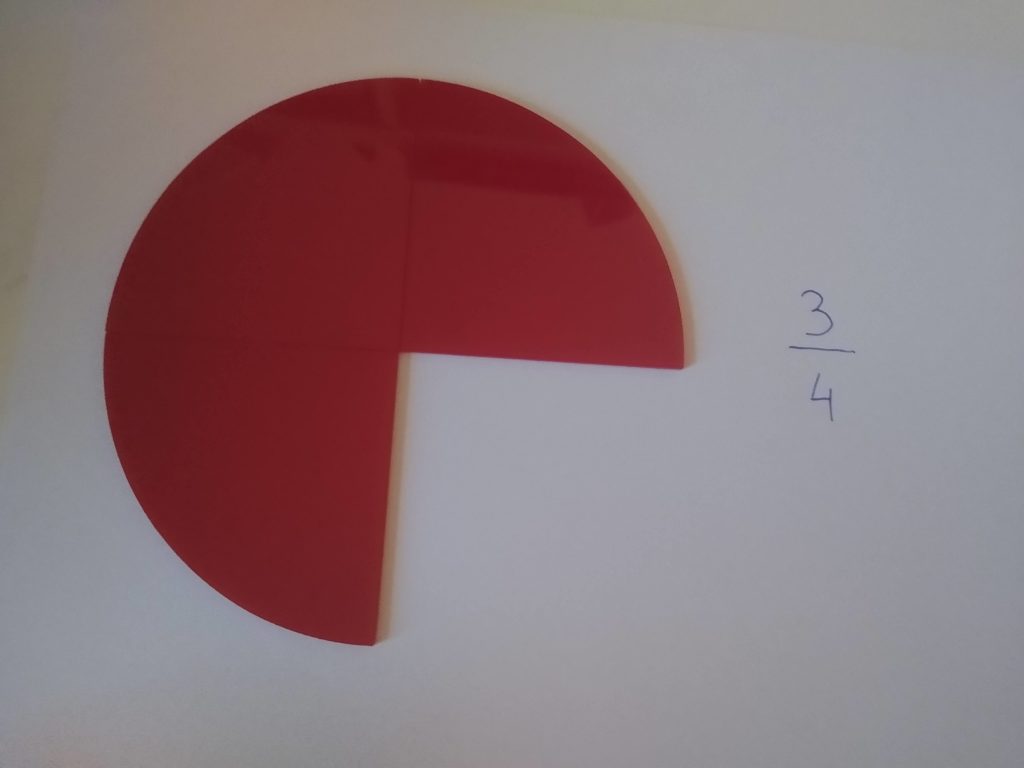
Pierwsze przekształcenia i działania na ułamkach

Stąd droga otwarta do dalszego poznawania – zwykle dziecko swoimi pytaniami pokieruje nas na kolejne etapy. Dzięki konkretowi, mamy już wszystko, co potrzebne, żeby:

• opisywać liczby wymierne większe od 1 za pomocą liczb mieszanych lub ułamków niewłaściwych,
• zamieniać liczby mieszane na ułamki niewłaściwe (i odwrotnie),
• porównywać ułamki o takich samych mianownikach,
• porównywać ułamki o takich samych licznikach,
• dodawać i odejmować ułamki o takich samych mianownikach,
• rozszerzać i skracać ułamki, …

… ale o tym już w kolejnych wpisach 🙂

Najważniejsze jest to, że ułamki zwykłe mogą być dla dzieci rzeczywiście “zwykłe” i przystępne – im wcześniej zaczną z nimi pracować, tym łatwiej będzie im dostrzegać różne zależności, by później przejść do tych bardziej skomplikowanych. Dzięki pracy na konkrecie nawet odejmowanie przy różnych mianownikach i dzielenie mogą być zrozumiałymi (zamiast wyuczonymi na pamięć) działaniami.