Pokazywałam już, jak można zbudować bryły foremne i jak można zaskakująco wykorzystać dwudziestościan. Ale to dopiero początek tego, co można zobaczyć w wielościanach foremnych! Zapraszam na małe i duże przygody pełne zaskoczeń 🙂
Na początek spróbujemy przyjrzeć się liczbie ścian, krawędzi i wierzchołków każdego wielościanu foremnego. A co to właściwie jest?
- ściany to wielokąty tworzące wielościan,
- krawędzie to odcinki, będące bokami ścian (każda krawędź leży “pomiędzy” dwoma ścianami),
- wierzchołki to punkty, które są końcami krawędzi (w każdym wierzchołku tych krawędzi schodzi się kilka, co najmniej trzy).
Spróbujcie je policzyć. Ile ścian, krawędzi i wierzchołków jest w każdym z wielościanów foremnych? Wcale nie jest to takie łatwe zadanie (szczególnie w dwunastościanie i dwudziestościanie). Czy te liczby mają ze sobą jakiś związek? Ano, mają! 🙂
Przygotowałam karty pracy do pobrania (jak zwykle wraz z kartami kontrolnymi), dzięki którym dzieci mogą te zależności zauważyć. Mam nadzieję, że kolejnym krokiem będzie próba wyjaśnienia “dlaczego?”. O tym też za chwilę napiszę 🙂
Najpierw jednak o samych kartach. Dla każdej z brył stworzyłam oddzielną kartę pracy o takiej samej budowie. Wszystko poza rysunkiem i nazwą bryły jest jednakowe. No i jeszcze poza… końcówkami wynikającymi z odmiany w języku polskim 🙂 Te końcówki mogą stanowić dla dziecka częściową kontrolę błędu. Zaczynamy od uzupełnienia liczby ścian (np. w sześcianie ścian jest 6) oraz liczby boków każdej z nich (w moim przykładzie ściany to kwadraty, mają po 4 boki). Dalej uzupełniamy liczbę krawędzi (dla sześcianu jest to 12 – jeśli położymy sześcian na jednej ze ścian, to 4 krawędzie są jej bokami, 4 znajdują się przy przeciwległej ścianie i 4 “pomiędzy”). Następnie liczymy wierzchołki (sześcian ma ich 8 – 4 jest jednej ze ścian i 4 przy przeciwległej) oraz to, ile krawędzi wychodzi z każdego wierzchołka (w wierzchołku sześciany łączą się 3 krawędzie). Co teraz? Zgodnie ze zdaniami przy strzałkach mnożymy odpowiednie liczby: liczbę ścian przez liczbę boków każdej z nich (w sześcianie jest to 6×4=24), liczbę krawędzi mnożymy przez 2 (12×2=24) oraz liczbę wierzchołków mnożymy przez liczbę krawędzi schodzących się w każdym z nich (8×3=24).
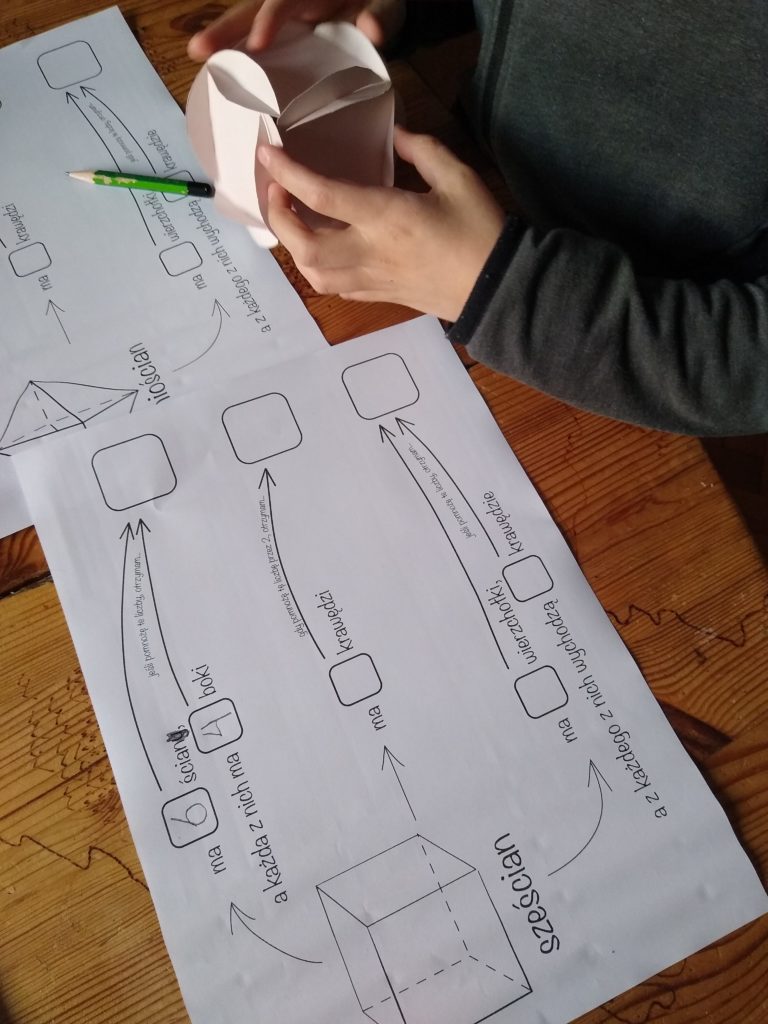
Gdy widzimy trzy jednakowe liczby (to znowu częściowa kontrola błędu, jeśli dziecko pracuje z nimi po raz kolejny) na pierwszej karcie, możemy myśleć o przypadku (choć dzieci obcujące z pomocami Montessori raczej w nie nie wierzą ;)). Po uzupełnieniu wszystkich kart mamy już mocne przekonanie, że musi za tym stać jakaś zasada. I rzeczywiście! Tak naprawdę są to dwie zasady, które po małej zmianie opisują zależności w dowolnym wielościanie. Najprostszą formę przyjmują w wielościanach foremnych, właśnie ze względu na to, że każda ściana ma tyle samo boków, i z każdego wierzchołka wychodzi tyle samo krawędzi.
Najpierw odkryjemy, dlaczego pierwsze dwie liczby po prawej stronie będą jednakowe. Opiszę to na przykładzie sześcianu, ale dokładnie w ten sam sposób można dostrzec to w każdym wielościanie foremnym. W tym celu przypatrzymy się naszym wielościanom zbudowanym z kół (jeśli ich nie znacie, zapraszam do wcześniejszego wpisu). Każde koło jest tam podzielone na wielokąt i odcinki kołowe. W przypadku sześcianu mamy koło złożone z kwadratu i czterech odcinków kołowych. Spróbujemy obliczyć liczbę tych odcinków kołowych we wszystkich kołach użytych do budowy sześcianu. Z jednej strony w każdym użytym kole jest ich cztery, a kół jest sześć, tyle co ścian. Liczba odcinków kołowych to nic innego jak wynik mnożenia tych liczb, czyli górna liczba po prawej stronie karty sześcianu. Z drugiej strony przy każdej z dwunastu krawędzi sześcianu łączyliśmy dwa odcinki kołowe, więc ich liczba to dwukrotność liczby krawędzi (to właśnie środkowa liczba po prawej stronie karty). W takim razie dwie liczby po prawej stronie opisują liczbę odcinków kołowych we wszystkich użytych kołach i muszą być równe! 🙂
Spróbujemy teraz pokazać, że środkowa i dolna liczba są równe. Tym razem spróbujemy to zrobić, budując szkielety wielościanów z wykałaczek. Możemy łączyć je w każdym wierzchołku za pomocą dowolnej w miarę gęstej masy (masa solna sprawdza się dość dobrze w mniejszych bryłach) lub klejem na gorąco. Dwunastościan i dwudziestościan są dość trudne do uzyskania, ale możemy spróbować z mniejszymi wielościanami, a potem skorzystać z mocy wyobraźni 😉

Jeśli mamy już gotowy wielościan, spróbujmy przeciąć każdą z wykałaczek na pół. Ile mniejszych patyczków powstanie? Oczywiście jest ich dwa razy więcej niż krawędzi (a więc środkowa liczba na naszej karcie!). Z drugiej strony, możemy przyjrzeć się temu, co zostało z naszego wielościanu. Otrzymaliśmy części, a w centrum każdej z nich znajduje się dawny wierzchołek wielościanu (jest ich tyle co wierzchołków), a z niego wystaje zawsze jednakowa liczba patyczków (taka jak liczba krawędzi wychodzących z każdego wierzchołka). To oznacza, że liczba patyczków jest iloczynem liczby wierzchołków i liczby krawędzi wychodzących z jednego wierzchołka – to nasza “dolna” liczba na karcie!

Mam nadzieję, że czujecie się przekonani, że to nie przypadek, ale po prostu kilka różnych sposobów zliczania tego samego. Taka metoda dowodzenia pewnych zależności w matematyce wcale nie jest taka rzadka 🙂 Jeśli ma przerodzić się w formalny dowód, wystarczy w przyszłości zapisać ją w ogólny sposób i doprecyzować różne intuicje. Te poznane zależności to zresztą nie koniec! Jest ich więcej, ale o tym już następnym razem… będziecie chcieli poczytać?







