Pokazywałam już, jak mnożyć przez liczbę jednocyfrową na znaczkach. Jest jednak jeszcze jeden etap przed przejściem do abstrakcyjnego mnożenia na kartce, bardzo charakterystyczny i kojarzony przez wielu z matematyką Montessori, a jest to szachownica do mnożenia. Jeśli po tym artykule dojdziecie do wniosku, że warto ją mieć, możecie rozważyć wydrukowanie jej na tkaninie. Ale zaczynajmy!
Co będzie nam potrzebne?
Nie obejdzie się bez szachownicy 😉 Jeśli jeszcze jej nie masz, po prostu wytnij ciemnozielone, granatowe i czerwone kwadraty i sklej je ze sobą na wzór dolnego rzędu szachownicy (to wystarczy do mnożenia przez liczbę jednocyfrową).
Niezbędne będą też kolorowe liczby. Takie, które zmieszczą się na polach szachownicy. Ja używam zakupionych, ale mogą to być też kolorowe perły czy wydrukowane kolorowe liczby.
Przydadzą się również kafelki z cyframi. Tradycyjnie są to cyfry w kolorach odpowiadającym polom szachownicy. Jeśli nie macie możliwości – takie czarno-białe też nadadzą się doskonale! Polecam wydrukować je na sztywnej kartce lub nakleić na coś sztywnego (ja zdecydowałam się na kwadraty ze sklejki). Tym razem kafelki są jednostronne – to celowo! Warto umieścić je w pudełku z przegródkami – każdy kolor oddzielnie, ale też nie jest to konieczne. Jeśli chcecie je wydrukować, tutaj znajdują się odpowiednie pliki do druku:
-
 Kolorowe liczby0,00 zł
Kolorowe liczby0,00 zł -
 Kafelki do szachownicy do mnożenia0,00 zł
Kafelki do szachownicy do mnożenia0,00 zł
Zapisywanie i odczytywanie liczb na szachownicy
Zanim zabierzemy się za mnożenie, musimy umieć zapisywać i odczytywać liczby na szachownicy. Dziś będziemy je układać tylko w dolnym rzędzie. Każde z pól szachownicy odpowiada jednej z pozycji dziesiątkowej w liczbie. Po prawej stronie jest pole ciemnozielone, odpowiadające jednościom, dalej w lewo jest granatowe pole dziesiątek, potem czerwone pole setek itd. Dodatkowo każde pole jest odpowiednio podpisane.
Weźmy jeden z kolorowych liczb. Jeśli położymy je na pole jedności – będzie to liczba jeden. Jeśli umieścimy je na polu dziesiątek – będzie to dziesięć. Położone na polu setek będzie oznaczać sto. Podobnie jest z innymi kolorowymi liczbami – weźmy na przykład siedem. Na polu jedności będzie oznaczać siedem, ale już na polu dziesiątek będzie to siedemdziesiąt. Warto przećwiczyć ten etap z dzieckiem (np. dziecko może kłaść kolorową liczbę na różne pola, a my nazywamy, potem zamieniamy się rolami).
Teraz spróbujemy połączyć naszą wiedzę w układy z kilku kolorowych cyfr. Jeśli położymy pięć na polu setek, osiem na polu dziesiątek i dwa na polu jedności, to otrzymamy pięćset osiemdziesiąt dwa. Oczywiście nie wszystkie kolejne pola muszą być zapełnione – na przykład cztery na polu tysięcy i siedem na polu dziesiątek będzie oznaczało liczbę cztery tysiące siedemdziesiąt. Ten etap również warto przećwiczyć z dzieckiem (zarówno odczytywanie liczb ułożonych na szachownicy, jak i układanie z kolorowych liczb zadanej liczby).
Zamiany, czyli dziesiątki w akcji
Układając liczby używaliśmy tylko kolorowych liczb do dziewięciu. Teraz przyjdzie pora też na złote dziesiątki 🙂 Poza samym zapisywaniem liczb potrzebna nam będzie też wiedza, jak możemy wymienić większe wartości, które znajdą się na polach w czasie mnożenia.
Zacznijmy od poproszenia dziecka by ułożyło liczbę 10 na szachownicy (powinno położyć jeden na polu dziesiątek). Teraz zabierzmy liczbę ułożoną przez dziecko i połóżmy dziesiątkę na polu jedności – co to za liczba? To dziesięć jedności, czyli… dziesięć! Jeden na polu dziesiątek i dziesięć na polu jedności oznaczają dokładnie to samo (przypomina to “rozmienianie” złotego materiału albo znaczków, bo… to jest właśnie dokładnie to samo! tylko inaczej zapisane ;)).
Spróbujmy podobny proces przejść z jeden na polu setek i dziesiątką na polu dziesiątek (tutaj pewnie potrzebna będzie chwila zastanowienia, że dziesięć dziesiątek to jedna setka). Podobnie możemy zrobić z jeden na polu tysięcy i dziesiątką na polu setek. I tak dalej 🙂 Kluczowym wnioskiem dla dziecka jest to, że jeśli pojawi się dziesiątka na jakimś polu, to możemy “zamienić” ją na jeden na polu następnym w lewo.
Teraz pobawmy się znowu w odczytywanie liczb, ale tym razem kładźmy na jednym polu więcej niż jedną kolorową liczbę. Opiszę to na poniższym przykładzie, pokażę jak odczytać liczbę ze zdjęcia:



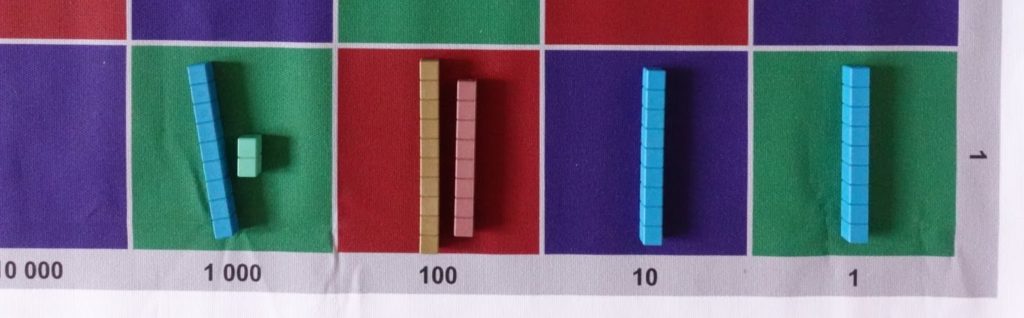



Teraz możemy już odczytać naszą liczbę: jedna dziesiątka tysięcy, dwa tysiące, osiem setek, dziewięć dziesiątek i dziewięć jedności, czyli dwanaście tysięcy osiemset dziewięćdziesiąt dziewięć.
Ruszamy z mnożeniem
Mnożenie przez liczbę jednocyfrową najlepiej wprowadzać, stopniując trudność. Dobrze nadadzą się do tego przygotowane przeze mnie Bazy. Na pierwszym etapie wykorzystamy przykłady z Bazy 23, czyli takie bez przekraczania progu dziesiątkowego.
Przypomnijmy dziecku, że mnożenie oznacza kilkukrotne branie danej liczby i zliczanie “ile to jest razem”. Spróbujemy wykonać mnożenie liczby 132 przez 3. Zacznijmy od ułożenia liczby 132 z kafelków pod polami szachownicy (jeśli mamy kolorowe kafelki, zadbajmy o zgodność tych kolorów z polami szachownicy). Po prawej stronie dolnego rzędu układamy kafelek z cyfrą 3, bo to właśnie przez liczbę 3 będziemy mnożyć.

Teraz przystępujemy do mnożenia. Za pierwszym razem poprośmy dziecko o ułożenie liczby 132 na szachownicy. Teraz kładziemy jeszcze dwie takie liczby (razem musimy mieć trzy kopie).

Żeby obliczyć wynik mnożenia wystarczy odczytać, jaka liczba leży teraz na szachownicy. Kilka zamian i już wiemy: otrzymaliśmy trzysta dziewięćdziesiąt sześć:
Kolejne etapy
Na kolejnym etapie, któremu mogą towarzyszyć przykłady z Bazy 24, pojawia się przekroczenie progu dziesiątkowego, na początku w jednym tylko miejscu. Dla dziecka będzie to połączenie dwóch umiejętności, które już ma – jeśli obie opanowało, to powinno szybko poradzić sobie z opanowaniem tej umiejętności.
Jak w praktyce wygląda mnożenie z przekroczeniem progu na szachownicy? Tak samo! Jedyną różnicą jest to, że w momencie zliczania na jednym z pól pojawi się liczba większa od 9 (wartą ją ułożyć za pomocą dziesiątek i co najwyżej jednej innej kolorowej liczby). Możemy dziesiątki z tego pola zamienić na odpowiednią kolorową liczbę na polu z lewej strony (np. jeśli były trzy dziesiątki na polu setek, to zamieniamy je na trzy na polu tysięcy). Ważne, by jednocześnie pokazać dziecku zapis pisemnego mnożenia w takiej sytuacji – “przenoszoną” cyfrę zapisujemy na górze nad odpowiednią cyfrą czynnika.
Kolejny etap, zawarty w bazie 25, to wielokrotne przekraczanie progu. Nie różni się od poprzedniego etapu, poza tym, że “przeniesienie” będziemy wykonywać kilkukrotnie. Opiszę w szczegółach mnożenie liczby 749 przez 4.







I już możemy odczytać wynik: dwa tysiące dziewięćset dziewięćdziesiąt sześć.
A co dalej?
Jeśli dziecko biegle oblicza iloczyny na szachownicy, warto poprowadzić go do wejścia na etap abstrakcyjnych obliczeń. Dalej wykonujemy podobne przykłady, po prostu robimy je stopniowo wykonując coraz mniej działań na materiale, a coraz więcej w głowie:
- Warto zacząć od tego, by układać na polach od razu wyniki z tabliczki mnożenia (np. zamiast czterech siódemek ułożyć od razu dwadzieścia osiem). Na tym etapie warto też od razu uczyć dziecko, by przy wykonywaniu obliczenia zakrywało odpowiedni kafelek pod szachownicą – bardzo nam to pomoże na przyszłość, żeby nie pogubić się, które mnożenia zostały już wykonane. Po wykonaniu mnożeń z wszystkich pól, dokonujemy odpowiednich zamian, by odczytać wynik.
- Na kolejnym etapie wykonujemy mnożenie z poszczególnych pól w głowie, ale od razu zamieniamy dziesiątki na odpowiednią kolorową liczbę na następnym polu, np. liczymy “cztery razy siedem to dwadzieścia osiem” i kładziemy osiem oraz dwa na polu po lewej stronie. Na samym końcu musimy dokonać pewnych zamian (bo dodajemy “przeniesienia” do wartości z odpowiednich pól), ale jest ich zdecydowanie mniej.
- Na ostatnim etapie dziecko od razu dodaje przeniesienia i ma gotowy wynik. Opiszę to w szczegółach, pomnożymy w ten sposób 875 przez 7:




Po takim mnożeniu mamy od razu gotowy wynik do odczytania: sześć tysięcy sto dwadzieścia pięć.
Doskonale widać też, że stąd tylko malutki krok do wykonania działania bez materiału. A przecież do tego dążymy – przez ręce docieramy do abstrakcji, która będzie działa się w głowie 🙂








2 komentarze “Szachownica – mnożenie przez liczbę jednocyfrową”
Przez ręce docieramy do abstrakcji. Piękne 🙂
Dzieki za wpis, bede zaraz korzystac:)
Bardzo dziękuję, Olu! Dobrego korzystania!