Poniżej przedstawiam wybrane elementy historii matematyki, uporządkowane w kolejności chronologicznej. Staram się każdy opatrzeć rysunkiem, by ułatwić wyszukanie tych interesujących nas (i naszych uczniów / nasze dzieci) i umożliwić wplecenie ich w opowieść.

(kilkanaście tysięcy lat temu) System karbowy
Ślady pierwszych prób zliczania przez człowieka pochodzą z okresu górnego paleolitu. Na kościach (na rysunku znajduje się kość z Ishango) umieszczał przy tym podłużne karby. Sposoby były różne, nie znamy również ich dokładnego zastosowania – naukowcy wskazują, że mogła to być analiza faz księżyca czy liczba posiadanych przedmiotów.
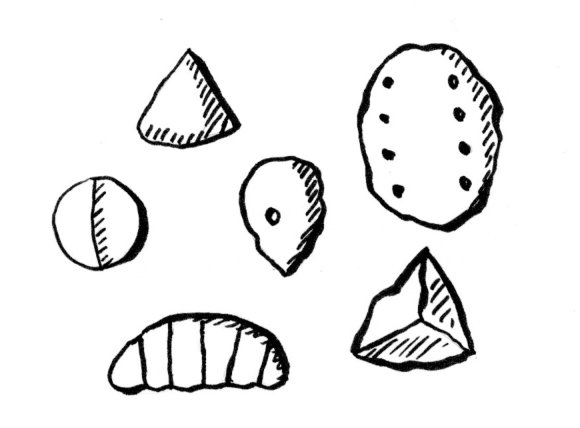
(8000 p.n.e.) Gliniane tokeny
Przed wynalezieniem pisma, na terenie Persji i Iraku, używano wypalanych z gliny tokenów o różnych kształtach. Najprawdopodobniej każdy rodzaj tokenów odpowiadał konkretnemu przechowywanemu towarowi czy hodowanemu zwierzęciu. Liczba tokenów odpowiadała ilości towaru czy zwierząt. System tokenów ewoluował – zwiększała się liczba ich rodzajów, a na ich powierzchni wykonywano różne nacięcia i żłobienia.

(3200 p.n.e.) Zapis liczb u Sumerów
Sumeryjski sposób liczenia oparty był na liczbach 60 i 10. Można powiedzieć, że był to system pozycyjny (choć nie w pełni z tego korzystali), ale cyfry (od 0 do 59) były zapisywane w glinie przy pomocy klina. Odpowiednio ułożony pozwalał uzyskać kreskę oznaczającą 1, natomiast ustawiony inaczej dawał “dzióbek” symbolizujący 10. Ich zestawienie pozwalało zapisać liczby od 1 do 59 (na rysunku można zobaczyć kolejno 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 20, 30, 40 i 50). Aby zapisać większą liczbę, trzeba było najpierw zapisać, ile mieści się w niej pełnych sześćdziesiątek, a następnie pozostałą część liczby. W ten sposób dawało się zapisać wszystkie liczby poniżej 3600! Większe również można było zapisać – najpierw pisząc ile pełnych liczb 3600 mieści się w naszej liczbie, następnie ile sześćdziesiątek trzeba do tego dodać, a na koniec resztę.
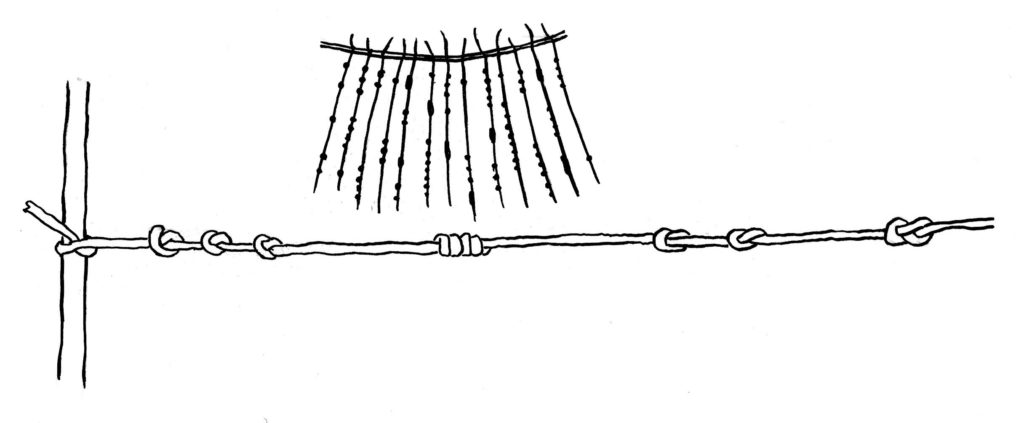
(3000 p.n.e.) Pismo węzełkowe (kipu) u ludu Caral
Kipu to sposób przechowywania informacji za pomocą węzełków na sznurach. Do głównego sznura dowiązujemy boczne, a na każdym z nich możemy zapisać część informacji (np. liczbę lub kilka liczb). Do dziś przetrwało niewiele oryginalnych kipu, niestety były niszczone w czasie kolonizacji terenów dzisiejszego Peru. Wieler wskazuje jednak na to, że używał go już lud Caral, żyjący tam około pięć tysięcy lat temu. Przez wiele wieków nic więcej nie było potrzebne – żyjące tam ludy w zasadzie aż do kolonizacji nie wykształciły tradycyjnego pisma.
Jak oznaczano węzełkami liczby? Węzły (lub grupy węzłów) na bocznych sznurkach były robione w równych odstępach. Każdy kolejny fragment oznaczał kolejną cyfrę w zapisie dziesiętnym liczby.
Cyfry inne niż jedności zapisywano, robiąc odpowiednią liczbę pojedynczych węzłów jeden za drugim. Cyfra jedności była zapisywana długim węzłem z odpowiednią liczbą oplotów, lub węzłem ósemkowym, gdy była to cyfra 1 (dlatego że długi węzeł z jednym oplotem jest tym samym co jeden prosty węzeł). Puste miejsce odpowiadało zawsze cyfrze 0. Dzięki wyróżnieniu jedności, zawsze wiadomo było, gdzie kończy się zapis jednej liczby, a zaczyna kolejny – w ten sposób jeden boczny sznurek mógł pomieścić kilka liczb.
Na rusynku na sznurku zapisane są dwie liczby: 34 i 21.
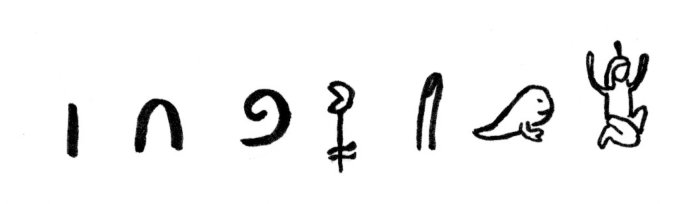
(2900 p.n.e.) Zapis liczb u Egipcjan
Egipcjanie do pisania używali hieroglifów. Około trzeciego tysiąclecia p.n.e. wykształciły się specjalne hieroglify do zapisu liczb. Były to: kreska (odpowiadająca liczbie 1), pęta (10), zwój liny lub liść palmy (100), kwiat lotosu (1000), palec wskazujący (10000), żaba (100000) oraz postać z podniesionymi rękoma (1000000). Liczbę zapisywało się zestawiając odpowiednią liczbę poszczególnych symboli (nie więcej niż 9 jednego rodzaju). Jest to pierwszy znany system dziesiętny, ale nie jest on systemem pozycyjnym (w którym ta sama cyfra może mieć różne znaczenie w zależności od pozycji w liczbie).
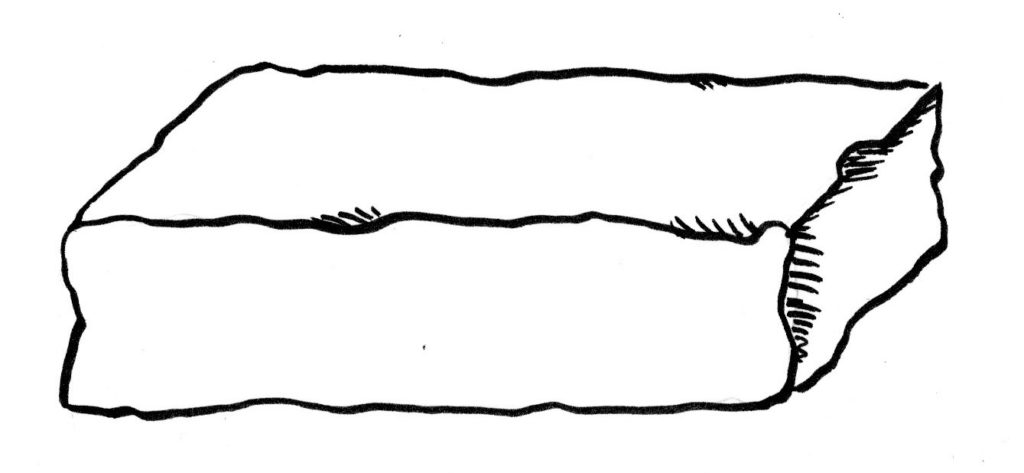
(2800 p.n.e.) System dziesiętny w dolinie Indusu
Z tego czasu pochodzą pierwsze znane ślady użycia w tamtych rejonach systemu miar długości, opartego na systemie dziesiątkowym. Najmniejsza używana jednostka miała mniej niż 2mm długości, pomiary były więc stosunkowo precyzyjne. Pomiary były wykorzystywane między innymi do wyrobu cegieł – prawie wszystkie cegły pochodzące z tamtego okresu w dolinie Indusu, mają stosunek wymiarów 4:2:1. Takie proporcje są do dziś uważane za jedne z najlepszych do budowy. Niezwykłą precyzją

(2600 p.n.e.) Sumeryjskie tabliczki działań arytmetycznych
Z tego okresu pochodzą tabliczki, zawierające dość pełne zestawienie działań arytmetycznych, pozwalających na odtworzenie procesu ich obliczania przez Sumerów. Dodawanie i odejmowanie jest w ich systemie zapisu prostym działaniem (wykonywanym podobnie, jak robimy je dzisiaj). Mnożenie wykonywali przez podwajanie (opisane poniżej w analogicznej wersji egipskiej). Dzielenie polegało tak naprawdę na mnożeniu dzielnika przez kolejne liczby tak długo, aż wyszła dzielna.
Co ciekawe, na tabliczkach sumeryjskich znaleziona została również tablica kwadratów i sześcianów (na rysunku powyżej).

(1900 p.n.e.) Pierwsze ślady działań arytmetycznych w Egipcie
Z tego czasu pochodzą najstarsze zapisy hieroglificzne, które zawierają dostateczną liczbę działań arytmetycznych, byśmy mogli zrozumieć, jak były wykonywane. Dodawanie i odejmowanie było wykonywane podobnie jak dzisiaj. Mnożenie opierało się o tablicę podwajania (analogiczną jak u Babilończyków), jak na rysunku. Więcej na ten temat można przeczytać w jednym z zadań rozszerzających Wielką Opowieść o Historii Liczb, którą możecie pobrać na stronie Opowieści.
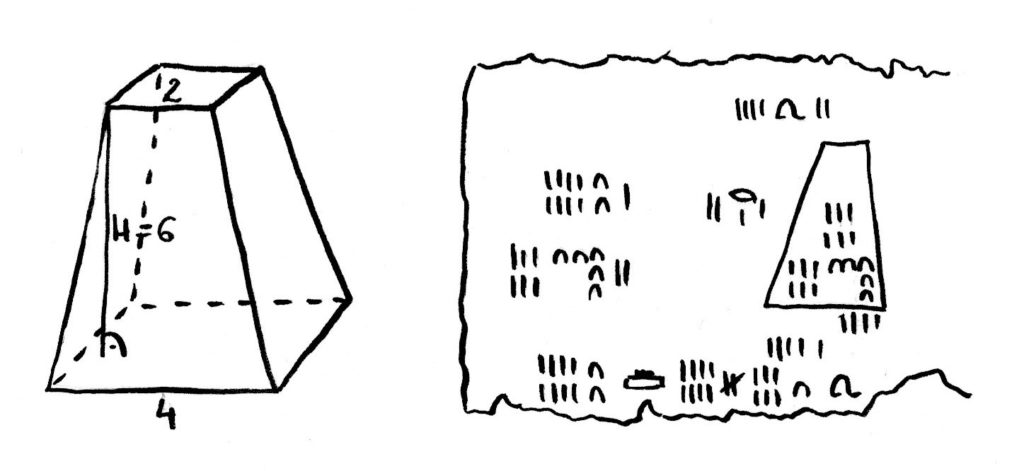
(1850 p.n.e.) Obliczanie objętości ściętego ostrosłupa
Z tego czasu pochodzi papirus pochodzący ze starożytnego Egiptu, który badacze nazwali papirusem moskiewskim. Zawiera rozwiązania równań oraz wielu praktycznych problemów. Jednym z nich było obliczenie ściętego ostrosłupa (jak na rysunku – kwadratowe podstawy mają boki 2 i 4, a wysokość jest równa 6). Zachęcam do tego, by osoby znające wzór na objętość stożka, spróbowały same obliczyć tą objętość!
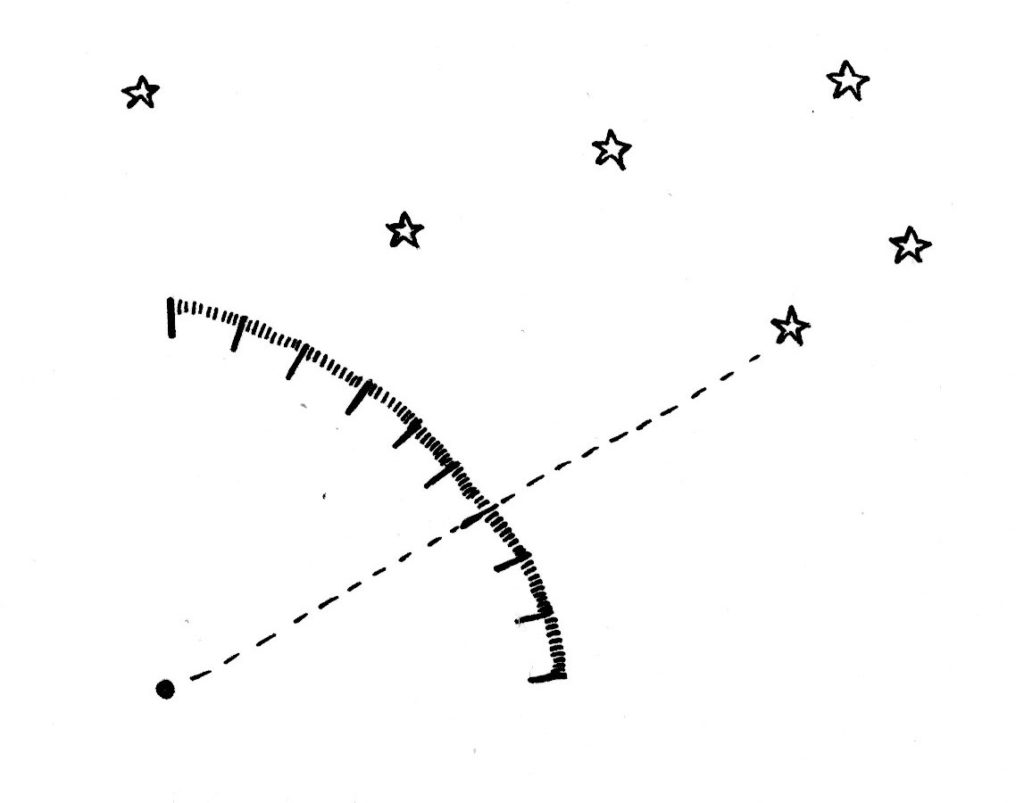
(1800p.n.e.) Ułamki i równania w Babilonii
Z tego czasu pochodzą pierwsze tabliczki, na których Babilończycy mierzyli się z ułamkami i równaniami.
Ułamki w zapisie Babilończyków to ułamki w systemie sześćdziesiętnym (odpowiednik naszych ułamków dziesiętnych). Po zapisaniu całości, zapisywano części 60-tne, 3600-tne, 216000-ne itd. Co ciekawe, Babilończycy nie wprowadzili znaku odpowiadającego naszemu przecinkowi – widząc cyfry 5 i 21 obok siebie, czytający musiał domyślić się z kontekstu, czy zapisana liczba to 5*60+21=321, czy może 5+21/60, czy jednak 5/60+21/3600.
To dzięki rozszerzeniu systemu sześćdziesiętnego na ułamki Babilończycy mogli liczyć na nich znacznie szybciej i dokładniej, niż Egipcjanie. To właśnie temu zawdzięczamy ich ogromne osiągnięcia w algebrze czy astronomii. Po wprowadzeniu znaku pustego miejsca (odpowiednik naszego 0) przez Ptolemeusza, system ten utrzymał się w astronomii bardzo długo – na babilońskich ułamkach liczył jeszcze Mikołaj Kopernik!
Do dziś pozostałość sześćdziesiętnego systemu liczbowego mamy między innymi w podziale kąta pełnego na 360 stopni czy w jednostkach czasu (godzina to 60 minut, minuta to 60 sekund).
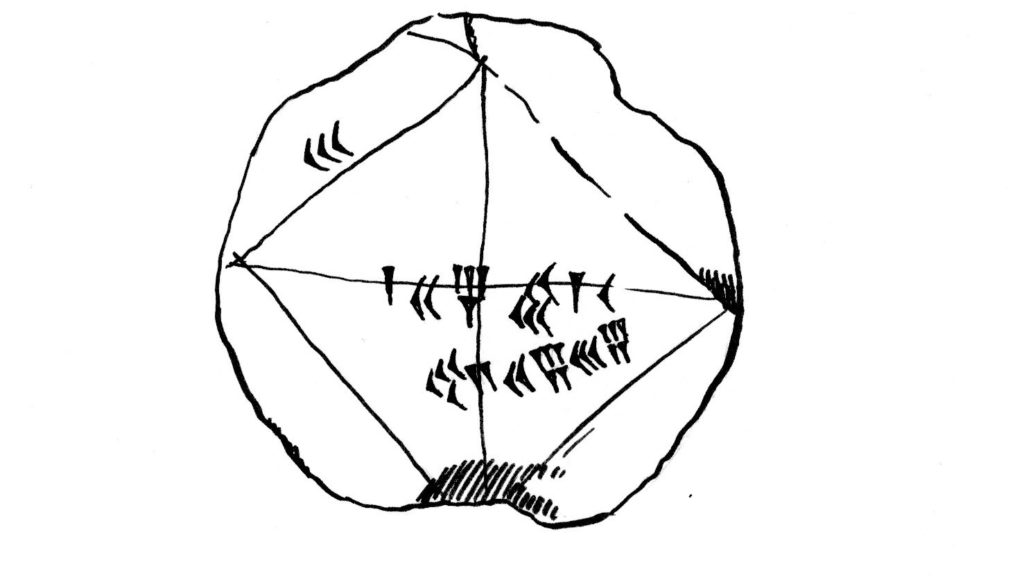
(1700 p.n.e.) Pierwiastek z 2
Gliniana tabliczka nazwana przez badaczy YBC 7289, zawiera narysowany w Babilonii kwadrat z przekątnymi oraz 3 liczby. Jedna z nich to wartość pierwiastka z 2 (potrzebnego do obliczenia długości przekątnej kwadratu o zadanym boku), pozostałe to 30 (długość boku) oraz 30 pomnożone przez pierwiastek z 2 (długość przekątnej).
Wartość pierwiastka z 2 została wyrażona na tabliczce jako 1+24/60+51/3600+10/216000=305470/216000, co różni się od znanej dziś wartości dopiero na 6 miejscu po przecinku (o mniej niż jedną milionową!).

(1650 p.n.e.) Papirus z Lahun – tablica ułamków
Egipcjanie korzystali z ułamków – jeśli nad liczbą był umieszczony znak ust (czasem tylko nad jej częścią, jeśli liczba jest duża), to było wiadomo, że chodzi o odwrotność tej liczby (czyli ułamek zwykły: jeden przez tą liczbę). Co ciekawe, Egipcjanie nie zapisywali ułamków o licznikach większych niż 1! Zamiast 2/3 zapisywali 1/2+1/6. Zamiast 4/5 pisali na przykład 1/2+1/4+1/20 (przedstawienie takie nie musi być jednoznaczne – może być kilka sum, dających ten sam wynik). Nam wydaje się skomplikowane, ale Egipcjanie byli w obliczeniach na takich ułamkach bardzo biegli, choć niestety obliczenia były czasochłonne i łatwo było o pomyłkę. Papirus z Lahun zawierał systematyczny egipski zapis ułamków równych ułamkom zwykłym o liczniku 2 i mianownikach nieparzystych od 3 do 101. Zachęcam do próby znalezienia takich sum, kilka pierwszych znajdziecie na rysunku 🙂 Pełne zestawienie z papirusu można znaleźć na stronie https://www.mtholyoke.edu/courses/mpeterso/math114/2013/Class2.html.
Istnienie zapisu każdego ułamka zwykłego na sumę różnych ułamków egipskich udało się udowodnić dopiero Fibonacciemu w 1202r. Nie przeszkadzało to jednak Egipcjanom w korzystaniu z takiego zapisu wszędzie tam, gdzie potrzebowali, ponieważ w praktyce potrafili taki rozkład znaleźć, używając opisanej powyżej tablicy. Jeśli chcieli na przykład zapisać 5/7, to zastępowali to przez 2/7+2/7+1/7. Następnie każde 2/7 zastępowali zgodnie z tablicą przez 1/4+1/28 i otrzymywali po uporządkowaniu w naszym języku 2/4+2/28+1/7. Biegły Egipcjanin wiedział, że 2/4=1/2 oraz 2/28=1/14 i otrzymywał szukany zapis: 5/7=1/2+1/14+1/7.
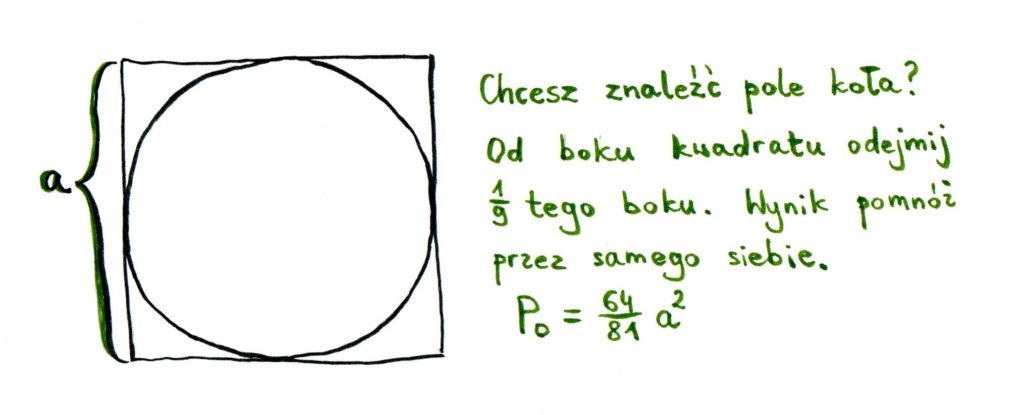
(1550 p.n.e.) Papirus Rhinda – upraszczanie ułamków i liczba π
Papirus Phinda zawierał bardzo wiele rozważań matematycznych. Część była poświęcona studiowaniu ułamków – poza zadaniami, znajduje się w nim między innymi tabela egipskiego zapisu ułamków 2/10, 3/10, 4/10, 5/10, 6/10, 7/10, 8/10 i 9/10.
Ponadto papirus zawierał szereg zadań wymagających działań na ułamkach. Autor papirusu zapisał tam również (użytą w praktyce – nie podał jej wartości w takiej postaci, jak to Egipcjanin ;)) wartość liczby π = 256/81. Różni się ona od właściwej wartości liczby π o mniej niż jeden procent.
Przedstawione wraz z rozwiązaniami problemy, wykorzystywały również równania, pozwalały na obliczenie pól figur czy objętości różnych brył.
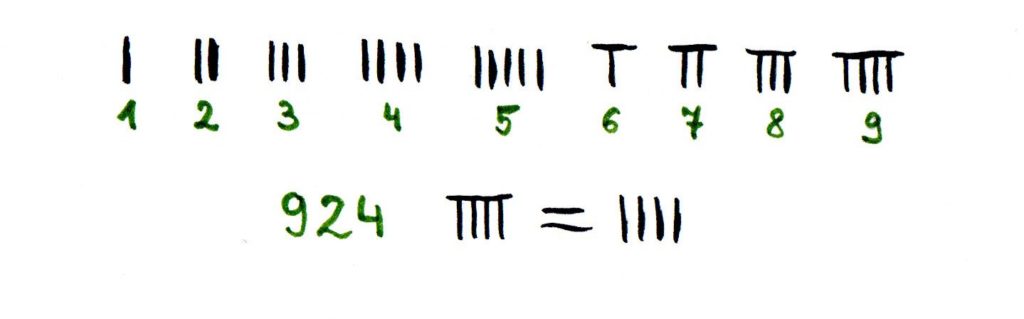
(1200 p.n.e.) Pierwszy znany zapis w dziesiętnym systemie pozycyjnym w Chinach
Matematyka w Chinach rozwijała się już dwa tysiące lat przed naszą erą. Do zapisu liczb używali bambusowych gałązek. Był to system dziesiętny używający 10 cyfr (na rysunku powyżej). Najwcześniejsze pisane liczby w systemie dziesiętnym, które przetrwały do naszych czasów, pochodzą mniej więcej z 1200r. p.n.e. Co ciekawe, cyfry w liczbie zapisywano na zmianę “normalnie” i “obrócone”.
(500 p.n.e) Magiczny kwadrat Luoshu w Chinach
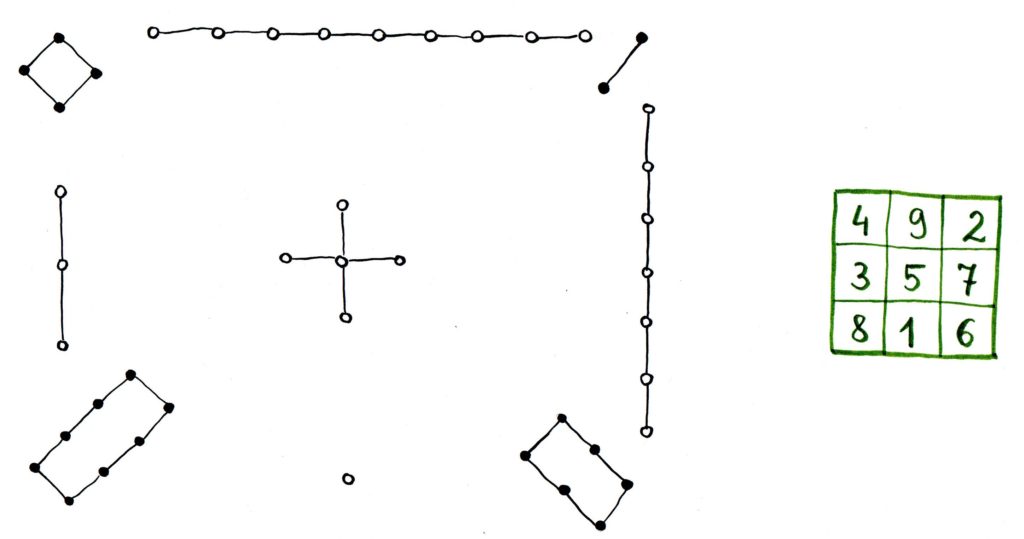
Z tego czasu pochodzi odnaleziony na terenie Chin kwadrat magiczny, w którym liczby w każdym wierszu, kolumnie i na przekątnych, sumują się do tej samej wartości. Jest on przedstawiony na rysunku, obok widnieje jego współczesna reprezentacja. Jego pochodzenie i symbolikę objaśnia legenda. Wiele jest też innych śladów, że w Chinach matematyka nie była jedynie nauką użytkową, ale również formą rozrywki.
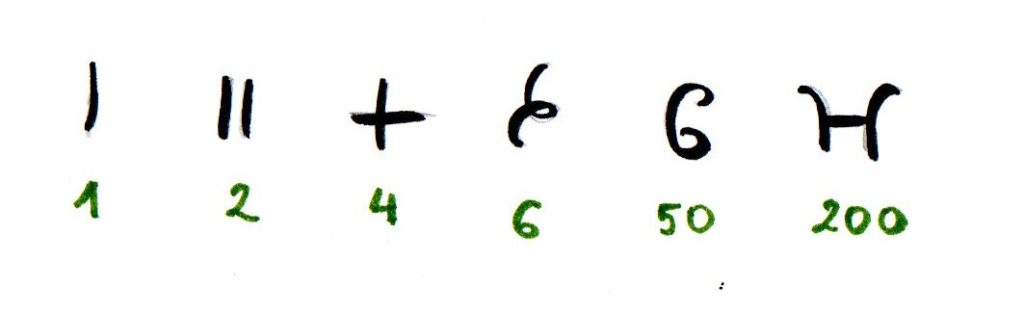
(300 p.n.e.) Na terenach Indii pojawia się pismo brahmi
Pismo brahmi z terenu dzisiejszych Indii zawierało również liczby w systemie dziesiątkowym. Nie był to jeszcze system pozycyjny (w którym znaczenie cyfry zależy od pozycji w liczbie) – 1, 10 i 100 było zapisywane za pomocą tych samych symboli. Znaki odpowiadające liczbom od 1 do 9 są najstarszym znanym pierwowzorem używanych dzisiaj przez nas cyfr arabskich.
(300 p.n.e.) W Mezopotamii pojawia się namiastka cyfry 0
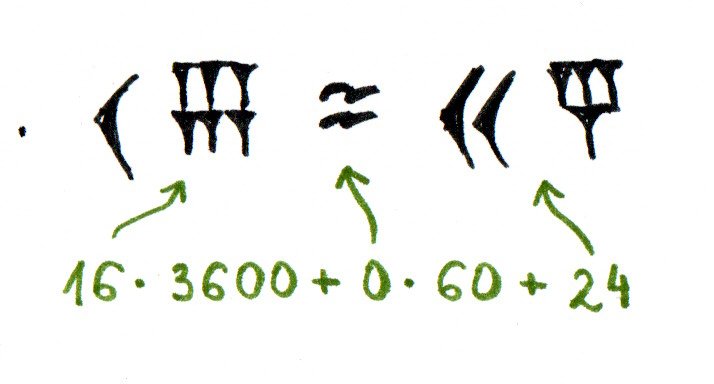
Babilończycy zaczęli używać dwóch falowanych kresek by zaznaczyć, że w zapisie liczby (w używanym przez nich systemie sześćdziesiątkowym) któraś cyfra jest równa 0. Wcześniej po prostu zostawiano puste miejsce, co nieraz prowadziło do pomyłek. Nadal jednak nie używali symbolu na końcu liczby (uważali, że z kontekstu wynika, czy zapis I oznacza 3600, 60, 1, czy może 1/60), ani jako samodzielnej liczby.
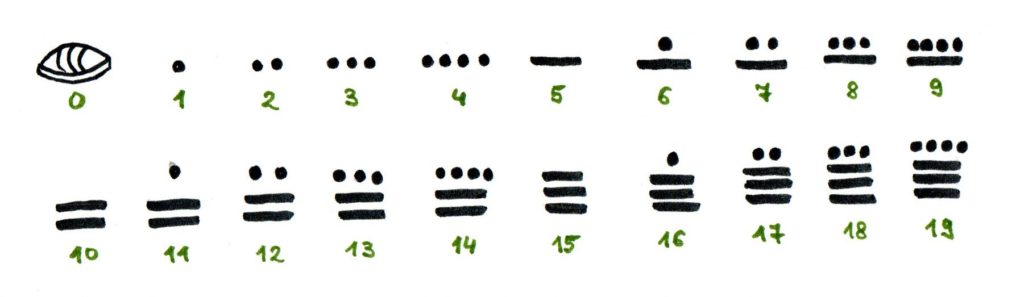
(250 p.n.e) Olmekowie używają cyfry 0
Lud Olmeków, żyjący na terenach Wyżyny Meksykańskiej, używał systemu dwudziestkowego, przejętego później przez Majów. Występuje w nich 0 jako pełnoprawna cyfra.

(1200) Szczegółowy kalendarz Majów
Z tego okresu pochodzi Kodeks Drezdeński, zwany tak od docelowego miejsca, w które trafił. Jest to dokument spisany przez skrybów Majów, choć najprawdopodobniej jest kopią dokumentu powstałego między V a IX wiekiem. Jest świadectwem kultury Majów, w szczególności rozbudowanego i niezwykle dokładnego kalendarza. Zawiera on między innymi informację, że rok trwa 365,242 dnia – Majowie znali go więc z błędem mniejszym niż kilkanaście sekund!
